Повышение конкурентоспособности продукции непосредственно связано с ее качеством. В силу ограниченных финансовых ресурсов повысить конкурентоспособность предприятия можно путем внедрения статистических методов управления качеством продукции при минимальных финансовых затратах. В данной статье на примере продукции строительного назначения рассматривается подход, заключающийся в применении функции потерь как одного из способов управления качеством продукции. Показано использование статистических методов контроля и управления при анализе качества продукции.
УДК 658.56
Т.В. УЧАЕВА, канд. экон. наук, доцент, кафедра «Экономика, организация и управление производством»,
Пензенский государственный университет архитектуры и строительства
Ключевые слова: управление качеством продукции, производство строительных материалов, статистические методы управления качеством, вариация, функция потерь, качественные показатели, финансовые затраты предприятия
Keywords: product quality management, production of building materials, statistical methods of quality management, variation, loss function, quality indicators, financial costs of the enterprise
Повышение конкурентоспособности продукции непосредственно связано с ее качеством [1]. В настоящее время существуют следующие рекомендации повышения конкурентоспособности предприятия [2]:
– проведение на предприятии инновационной политики;
– внедрение более совершенных форм выпускаемого товара;
– выпуск продукции, соответствующей государственным и мировым стандартам;
– расширение рынка сбыта продукции;
– использование только высококачественного сырья и материалов;
– постоянное повышение квалификации кадров;
– повышение материальной и моральной заинтересованности и улучшение условий труда работников;
– проведение маркетинговых исследований рынка и осуществление SWOT-анализа cвоего производства и конкурентов;
– инвестирование в научные разработки, направленные на повышение качества продукции;
– использование агрессивной рекламы.
В силу ограниченных финансовых ресурсов повысить конкурентоспособность предприятия можно путем внедрения статистических методов управления качеством продукции при минимальных финансовых затратах.
Безопасность и подтверждение соответствия продукции установленным требованиям задаются некоторыми ограничениями на значения показателей, например:
х ≥ хmin,
х ≤ хmax (1)
хmin ≤ х ≤ хmax
Любой выход за границы допуска приводит к браку продукции. Известно, что любой процесс изготовления связан с колебаниями его параметров. Но даже при отлаженном процессе вероятность получения брака составляет 0,27%.
Выпуск качественной продукции непосредственно связан с управлением производственными операциями, для чего требуется постоянный анализ состояния технологического процесса и внесение при необходимости корректировок. Очевидно, что решение поставленных вопросов невозможно без применения статистических методов контроля качества продукции [3-5]. Производство строительных материалов и изделий, как и любой технологический процесс, подвержен изменчивости, характер которой определяется различными факторами. При двухстороннем допуске наиболее оптимальное (целевое) значение контролируемого параметра – середина между пределами допуска. При этом вероятность получения качественной продукции составляет 99,73%. На рис. 1 показан процесс (кривая 1), когда среднее значение и среднее квадратическое отклонение (СКО) показателя качества гарантируют качественную продукцию, и процесс (кривая 2), при котором даже самое незначительное изменение показателя (снижение среднего или увеличение СКО) приведет к превышению допустимой доли дефектности.
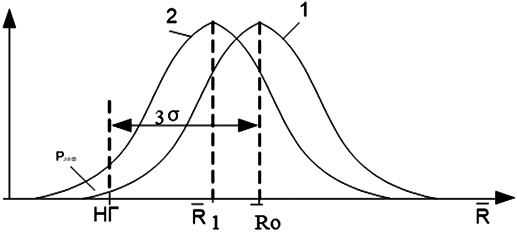
Предположим, что наблюдается сдвиг среднего значения показателя от середины поля допуска на 1,5σ [6]. Предположим, что партия продукции составляет 100 000 штук. Тогда количество продукции, показатели которой окажутся за контрольным пределом, будет составлять 13 360 [7]. Смещение процесса не приведет к появлению большого числа дефектов, если значение среднеквадратического отклонения позволяет, чтобы ±3σ уложилось в интервале от нижнего или верхнего контрольного предела до среднего.
По мнению японского ученого Генити Тагути, качество не может рассматриваться как мера соответствия требованиям нормативной документации [8].
Тагути предложил оценивать качество продукции функцией потерь L(yi), которая объединяет стоимостные и качественные показатели [9-11]:
L(yi)=k(yi-yo)2, (2)
где L – величина, учитывающая потери потребителя и производителя от бракованной продукции;
k – постоянная потерь;
y – значение измеряемого показателя;
y0 – оптимальное (целевое) значение показателя.
В соответствии с функцией Тагути, качество продукции может быть оценено по двум основным характеристикам: отклонение параметра качества y от требуемого значения y0 и разброс показателей качества [12-14].
Известно, что изменчивость свойств строительных материалов подчиняется нормальному закону распределения. Учитывая нормальный закон распределения и что поле допуска показателя качества содержит 6 сигм распределения, каждый показатель качества продукции предусматривает обеспеченность, равную 99,73% [15, 16]. Если качество продукции определяется несколькими характеристиками, то вероятность P получения качественной продукции составляет [17-19]:
P=q1* q2…qn, (3)
где q – вероятность соответствия требованиям нормативной документации i-го показателя.
Из этого следует важность учета при оценке качества продукции показателей отклонения параметра качества y от требуемого значения y0 и разброса показателей качества. Подходы к решению данной проблемы различны. В данной статье рассматривается подход, заключающийся в управлении качеством продукции с применением функции Тагути.
Предположим, что партия продукции состоит из N единиц. Тогда затраты, которые несет потребитель или изготовитель, могут быть определены по формуле:
L=kd2, (4)
где d2 – величина, равная
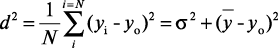, (5)
рассматривается как средний квадрат отклонения характеристики y от цели, определяющей уровень качества продукции.
В соответствии с формулой (2) потери определяются двумя источниками вариации: положением среднего арифметического значения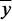 
относительно целевого значения y0 и разбросом значений показателя качества вокруг своего среднего значения 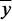, т. е. значением среднеквадратического отклонения σ.
Полная вариация SТ характеристики у определяется двумя компонентами [20-22]:
SТ=Sm+Se (6)
Компонента Se (фактор ошибки) определяется выборочной дисперсией
Se=(N–1)S (7)
Вторая компонента определяется значением выборочного среднего 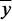относительно целевого значения yo и вычисляется в соответствии с выражением
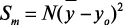(8)
Коэффициенты, учитывающие вклад каждого из факторов, определяются по формулам:
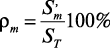, (9)
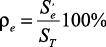, (10)
Рассмотрим применение функции потерь L(y) на примере кирпича керамического марки 100. Допустим, партия кирпича составляет 100 шт. Рассмотрим три варианта.
Вариант №1. По результатам выборки среднее значение предела прочности при сжатии не совпадает с серединой поля допуска и составляет Uд=111 кгс/см2, среднеквадратическое отклонение σ=5,3 кгс/см2.
Вариант №2. Среднее значение предела прочности при сжатии не совпадает с серединой поля допуска и составляет Uд=108 кгс/см2, среднеквадратическое отклонение σ=6,2 кгс/см2.
Вариант №3. Среднее значение предела прочности при сжатии совпадает с серединой поля допуска и составляет Uд=112,5 кгс/см2, среднеквадратическое отклонение σ=4,1 кгс/см2.
Анализ данных, приведенных в табл. 1, свидетельствует, что качество кирпича в 1-м варианте на 7,49% определяется положением истинного среднего и на 92,51% – разбросом значений прочности, т.е. фактором ошибки. Во втором варианте качество кирпича на 34,73% определяется положением среднего.
Таблица 1. Вариации показателя качества кирпича
| Источник вариации | Средний квадрат отклонения от цели, d2 | Вариация | Коэффициентвклада, ρ, % |
| 1 вариант | |||
| Положение среднего арифметического относительно середины поля допуска | 2,25 | 225 | 7,49 |
| Разброс показателей | 28,09 | 2780,91 | 92,51 |
| Суммарное | 30,34 | 3005,91 | 100 |
| 2 вариант | |||
| Положение среднего арифметического относительно середины поля допуска | 20,25 | 2025 | 34,73 |
| Разброс показателей | 38,44 | 3805,66 | 65,27 |
| Суммарное | 58,69 | 5830,56 | 100 |
| 3 вариант | |||
| Положение среднего арифметического относительно середины поля допуска | 0 | 0 | 0 |
| Разброс показателей | 16,81 | 1664,19 | 100 |
| Суммарное | 16,81 | 1664,19 | 100 |
В третьем варианте качество кирпича определяется на 100% разбросом значений прочности. Из этого следует, что производитель в первую очередь должен направить усилия на уменьшение разброса значений прочности кирпича. Для этой цели следует применять методы статистического регулирования технологических процессов [23-24].
Были рассчитаны финансовые затраты предприятия в зависимости от предполагаемого уровня дефектности (табл. 2). Стоимость кирпича составляет 8,8 руб./шт.
Таблица 2. Финансовые потери предприятия на 100 штук кирпича керамического
| № варианта | Вероятность появления дефектной продукции, % | Финансовые потери, руб., на 100 штук кирпича |
| 1 | 3,8 | 33,44 |
| 2 | 21,1 | 185,68 |
| 3 | 0,27 | 2,376 |
Результаты расчета (табл. 2) свидетельствуют, что чем ближе среднее арифметическое значение 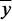к середине поля допуска y0 и чем меньше разброс показателей, тем меньше предприятие несет финансовые потери. Так, финансовые потери на 100 штук кирпича составляют 2,376 руб. (вариант №3) при значении среднеквадратического отклонения σ=4,1 кгс/см2 и 185,68 руб. (вариант №2) при значении среднеквадратического отклонения σ=6,2 кгс/см2
Вклад каждого составляющего в уровень качества продукции и финансовые затраты различен. Иногда затраты, связанные с уменьшением разброса значений характеристики yi вокруг своего среднего, оказываются более эффективными по сравнению с затратами, потраченными на наладку оборудования, в результате чего среднее совпадает с целевым значением y0 или оказывается близко к целевому значению y0. Производитель должен с учетом соответствующих коэффициентов вклада и финансовых затрат направить усилия организации в нужном направлении.
Выводы:
Показано применение статистических методов контроля и управления при анализе качества продукции. Рассмотрено использование функции потерь L(y) Тагути при анализе качества продукции. На примере кирпича керамического марки 100 рассчитаны финансовые затраты предприятия в зависимости от предполагаемого уровня дефектности. Выявлено, что финансовые затраты предприятия, связанные с уменьшением разброса значений характеристики yi вокруг своего среднего, оказываются более эффективными по сравнению с затратами, потраченными на наладку оборудования.
Показано, что чем ближе среднее арифметическое значение 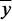к середине поля допуска y0 и чем меньше разброс показателей качества σ, тем ниже финансовые потери предприятия.
Применение анализа качества продукции с применением функции потерь Тагути позволит оптимизировать финансовые затраты предприятия с точки зрения рационального их назначения, что позволит предприятию при минимальных финансовых затратах повысить конкурентоспособность продукции.
Библиографический список
1. Мебадури З.А., Учаева Т.В. Управление качеством продукции как основной фактор конкурентоспособности строительной организации // Вестник БГТУ им. В.Г. Шухова, №9, 2018, с. 133-138.
2. Миронов М. Г. Ваша конкурентоспособность. – М.: Издательство «Альфа-Пресс», 2011, – 160 с.
3. Логанина В.И. К вопросу о регулировании технологических процессов производства бетона//Известия высших учебных заведений. Строительство, №3-4 (603-604), 2009, с. 42-45.
4. Логанина В.И., Учаева Т.В. К вопросу о системе контроля качества на предприятиях стройиндустрии // Региональная архитектура и строительство, №1, 2010, с. 31-33.
5. Логанина В.И., Хрусталева Б.Б., Учаева Т.В. Статистическое управление производством строительных изделий//Восточно-Европейский журнал передовых технологий, т. 1, №3 (61), 2013, с. 65-67.
6. Илей Л. Методы Тагути – мысль, облаченная в систему // Автомобильная промышленность США, №2, 1988, с. 20-22.
7. Гмурман В.Е. Теория вероятности и математическая статистика: Учебное пособие для вузов. – М.: Высшая школа, 1998.
8. Исикава К. Японские методы управления качеством: пер. с англ. / К. Исикава, ред. А.В. Гличева. – М.: Экономика, 1988, – 216 с.
9. Daniyan I.A., Mpofu K., Adeodu A.O. Optimization of welding parameters using Taguchi and response surface methodology for rail car bracket assembly // International journal of advanced manufacturing technology 2019 vol. 100. Issue 9-12 pp. 2221-2228 DOI: 10.1007/s00170-018-2878-9.
10. Bai Y., Wang H.Y., Wang L.K.; Tian K.K. Study and analysis on fuzzy quality control for the high-end manufacturing process based on Taguchi quality loss function//Journal of computational methods in sciences and engineering, 2019, vol., 19, issue 1, pp. 121-136 DOI: 10.3233/JCM-180857.
11. Брагин Ю.В. Инженерные методы повышения квалификации и снижения затрат по Генити Тагути. Выпуск 1. Функция потерь / Ярославль: Центр качества, 2005, – 68 с.
12. Mukhtarova K. S., Kozhakhmetova A. K.Statistical methods as a tool of high-tech products quality management / Bulletin of the national academy of sciences of the Republic of Kazakhstan. 2017, issue 3, pp. 243-250.
13. Vasilyeva Natalia, Koteleva Natalia, Ivanov Pavel. Quality analysis of technological process control//I. journal for quality research. 2018, vol. 12, issue 1, pp. 111-127.
14. Wang Youqing, Yabin Si, Biao Huang. Survey on the theoretical research and engineering applications of multivariate statistics process monitoring algorithms // Canadian journal of chemical engineering 2018, vol. 96, issue 10, pp. 2073-2085.
15. Коуден Д. Статистические методы контроля качества: Пер. с англ / Под ред. Б.Р. Левина. – М.: Изд-во физико-математической литературы, 1961.
16. Кузнецов Л.А.Оценка достоверности контроля рамочной технологии // Методы менеджмента качества, №3, 2007, с. 28-32.
17. Nsengiyumva Jean Baptiste; Luo Geping; Amanambu Amobichukwu Chukwudi. Comparing probabilistic and statistical methods in landslide susceptibility modeling in Rwanda/Centre-Eastern Africa // Science of the total environment. 2019, vol. 659, pp. 1457-1472.
18. Loganina V.I., Uchaevа T.V. Ensuring quality control reliability. Ensuring quality control reliability // J. Ponte – Jan 2017 – vol. 73, issue 1doi: 10.21506/j.ponte.2017.1.16.
19. Логанина В.И., Орентлихер Л. П. Повышение качества лакокрасочных покрытий строительных изделий и конструкций: Монография, – М.: Издательство Ассоциации строительных вузов, 2004, – 104 с.
20. Учаева Т.В. Применение статистического приемочного контроля при оценке качества кирпича керамического // Современные научные исследования и инновации, № 10, 2014 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/10/40033.
21. Luangpaiboon P.; Boonhao S.; Montemanni R. Steepest ant sense algorithm for parameter optimisation of multi-response processes based on taguchi design // Journal of intelligent manufacturing, vol. 30, Issue 1, 2019, pp. 441-457.
22. Ilgin Mehmet Ali. A spare parts criticality evaluation method based on fuzzy ahp and taguchi loss functions // Eksploatacja i niezawodnosc-maintenance and reliability, vol. 21, issue 1, 2019, pp. 145-152.
23. Учаева Т.В. Экономическая оценка качества процесса окрашивания строительных изделий и конструкций // Региональная архитектура и строительство, №4 (22), 2015, с. 132-136.
24. Qiu Yue, Wei Mingzhen, Bai Baojun. Descriptive statistical analysis for the PPG field applications in China: Screening guidelines, design considerations, and performances // Journal of petroleum science and engineering, vol. 153, 2017, pp. 1-11.
