УДК 691.42

В.И. ЛОГАНИНА, доктор техн. наук, профессор, заведующий кафедрой «Управление качеством и технология строительного производства», Пензенский государственный университет архитектуры и строительства

Ключевые слова: контроль качества, вероятность безошибочного прогноза, ошибка репрезентативности, керамический кирпич
Keywords: quality control, probability of an error-free forecast, error of representativeness, ceramic brick

Приведены сведения о значениях ошибки репрезентативности при оценке качества строительных материалов на примере кирпича керамического. Показано, что в правилах приемки соответствующего нормативного документа на строительную продукцию должно быть указано необходимое число образцов для испытания с учетом вероятности безошибочного прогноза.

При контроле качества строительных материалов в соответствии с действующей нормативной документацией проводят определение контролируемых параметров и сравнивают их с допускаемыми значениями. При выборочном контроле качества строительных материалов используют не всю генеральную совокупность, а только какую-то часть ее. По результатам измерения делается заключение о годности продукции и забраковке [1-4]. Однако полученный результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности.

Следует отметить, что в действующих нормативных документах на строительные материалы не указан показатель достоверности контроля. Достоверность контроля – это вероятность соответствия результатов контроля действительным значениям контролируемого параметра. В качестве оценок достоверности контроля качества строительных материалов вводятся понятия вероятности ошибок 1-го и 2-го рода. Ситуация, когда годное в действительности изделие по результатам контроля признается негодным («ложный брак»), называется ошибкой 1-го рода. И наоборот, ситуация, когда негодное в действительности изделие по результатам контроля признается годным («необнаруженный брак»), называется ошибкой 2-го рода. Вероятность получения верного результата контроля: РВ = 1 – (Р1 + Р2), где Р1и Р2 – вероятности ошибки 1-го и 2-го рода [5-7].

Показатели и средние величины должны служить отображением действительности, для чего необходимо определять степень их достоверности.

При проведении выборочных исследований результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность [8-11].

Ошибки репрезентативности могут быть случайными и систематическими. Случайные ошибки возникают из-за того, что совокупность отобранных единиц наблюдения неполно воспроизводит всю совокупность в целом. Систематические ошибки возникают вследствие нарушения принципов случайного отбора единиц изучаемой совокупности. Исследованию закономерностей случайных ошибок выборки посвящены предельные теоремы закона больших чисел. Наиболее полно эти закономерности раскрыты в теоремах П.Л. Чебышева и А.М. Ляпунова.

Для оценки ошибки репрезентативности применяют показатели средней ошибки выборки и предельной ошибки выборки.

Средняя ошибка признака при случайном отборе определяется по формуле:

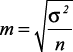, (1)

где σ – среднеквадратическое отклонение;
n – число наблюдений.

Предельная ошибка собственно-случайной выборки рассчитывается по формуле:

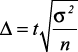, (2)

где σ² – дисперсия;
n – объем выборочной совокупности.

Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t. При вероятности безошибочного прогноза Р=99,7% значение t равно t=3, а при Р=95,5% – значение t=2.

Формула для определения доверительных границ средних величин имеет вид:

Хген=Хвыб±∆, (3)

где Xген – значения средней величины показателя генеральной совокупности;
Xвы6 – значения средней величины выборочной совокупности;
m – ошибка репрезентативности.

Ошибка репрезентативности и соответственно доверительные интервалы с определенной степенью вероятности безошибочного прогноза, как следует из (1), (3), определяются значением среднеквадратического отклонения и состоянием технологического процесса, т.е. стабильностью и воспроизводимостью [12-16].

Рассмотрим ошибку репрезентативности при контроле качества кирпича марки М100 в соответствии с действующей нормативной документацией. Согласно ГОСТ 530-2012 «Кирпич и камень керамические. Общие технические условия», определение среднего значения прочности на сжатие проводят при испытании 10 кирпичей. Рассмотрим 3 варианта.

1 вариант. По результатам выборки среднее значение предела прочности при сжатии не совпадает с серединой поля допуска и составляет Uд=111 кгс/см², среднеквадратическое отклонение σ=5,3 кгс/см².

2 вариант. Среднее значение предела прочности при сжатии не совпадает с серединой поля допуска и составляет Uд=108 кгс/см², среднеквадратическое отклонение σ=6,2кгс/см².

3 вариант. Среднее значение предела прочности при сжатии совпадает с серединой поля допуска и составляет Uд=112,5 кгс/см², среднеквадратическое отклонение σ=4,1кгс/см².

Результаты расчетов приведены в табл. 1

Таблица 1. Значение предельной ошибки выборки в зависимости от вероятности безошибочного прогноза Р

Наименование показателей	Номер варианта
	1	2	3
Средняя ошибка средней арифметической величины, МПа	1,7578	2,056	1,35
Вероятность безошибочного прогноза Р=95%
Доверительный интервал, МПа	107,48-114,52	103,89-112,11	109,8-115,2
Предельная ошибка выборки,МПа	3,5156	4,112	2,7
Вероятность безошибочного прогноза Р=99,73%
Доверительный интервал, МПа	105,73-116,27	101,83-114,17	108,45-116,55
Предельная ошибка выборки, МПа	5,2734	6,168	4,05

Установлено с вероятностью безошибочного прогноза Р=95%, что среднее значение прочности кирпича в партии (генеральной совокупности) будет находиться в пределах от 107,48 МПа до 114,52 МПа (1 вариант), т.е. среднее значение прочности кирпича в партии менее 107,48 МПа и свыше 114,52 МПа возможно не более чем у 5% случаев генеральной совокупности.

При вероятности безошибочного прогноза 99,7% среднее значение прочности кирпича в партии (генеральной совокупности) будет находиться в пределах от 105,73 МПа до 116,27 МПа (1 вариант), т. е. среднее значение прочности кирпича в партии менее 105,73 МПа и свыше 116,27 МПа возможно не более чем у 0,3% случаев генеральной совокупности. Если принять партию кирпича в количестве 1000 штук, то это составляет 30 штук кирпичей, у которых прочность при сжатии в партии менее 105,73 МПа и более 116,27 МПа.

Для определения необходимого объема выборки должны быть заданы предельная ее ошибка и вероятность того, что эта ошибка не превысит заданного предела. Расчет необходимого объема выборки может быть выполнен по формуле:

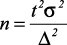. (4)

В соответствии с формулой (4), значение нормативной предельной ошибки ∆ должно определяться с учетом нормативного значения среднеквадратического отклонения. Учитывая, что в поле допуска показателя качества должно укладываться шесть сигм, т.е. шесть значений среднеквадратического отклонения, принимаем для кирпича марки М100 нормативное значение среднеквадратического отклонения, равное σ=4,1 МПа. Результаты расчета необходимой численности выборки для определения прочности при сжатии с учетом данных (3 варианта) приведены в табл. 2.

Таблица 2. Количество образцов для испытания прочности при сжатии керамического кирпича в зависимости от вероятности безошибочного прогноза Р

Номер варианта	Расчетное количество образцов для испытания при вероятности безошибочного прогноза Р=95%	Расчетное количество образцов для испытания при вероятности безошибочного прогноза Р=99,7%
1	7	16
2	10	21
3	4	10

Анализ данных, приведенных в табл. 2, свидетельствует, что только при вероятности безошибочного прогноза Р=99,7% при третьем варианте, когда значение среднеквадратического отклонения равно нормативному, количество образцов соответствует ГОСТ 530-2012 «Кирпич и камень керамические. Общие технические условия». Для 1-го и 2-го вариантов при вероятности безошибочного прогноза Р=99,7% количество образцов для испытания должно быть увеличено.

При вероятности безошибочного прогноза Р=95% количество образцов может быть уменьшено.

Таким образом, проведенные исследования и расчеты показывают, что в правилах приемки соответствующего нормативного документа на строительную продукцию должно быть указано необходимое число образцов для испытания с учетом вероятности безошибочного прогноза.

Библиографический список

1. Орлов А. И. Об оптимизации выборочного контроля качества продукции // Стандарты и качество, № 3, 1989, с. 382.
2. Зубкова Т.П. Совершенствование системы контроля качества в области экологической безопасности полимерных строительных материалов // Вестник ТГАСУ, №3, 2007, с. 195-203.
3. Тарасов Д.В., Тарасов Р.В., Макарова Л.В., Ермишина Я.А. Совершенствование контроля качества продукции строительного назначения // Современные проблемы науки и образования, № 1-1, 2015; URL: http://science-education.ru/ru/article/view?id=17591 (дата обращения: 20.09.2019).
4. Гончаренко О.А., Кочеткова М.В. Виды и методы контроля качества строительных работ защитно-отделочного цикла // Современные научные исследования и инновации, № 5, ч. 1, 2014, [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/05/34375 (дата обращения: 25.03.2019).
5. Головинский И.А. К обоснованию метода наименьших квадратов у П.Л. Чебышева // Историко-математические исследования. Колмогоров А.Н., Юшкевич А.П. (ред.) Математика XIX века. – М.: Наука. Том 1, Математическая логика. Алгебра. Теория чисел. Теория вероятностей. 1978.
6. Воронин В.Ф. Статистика: Учеб. пособие / В.Ф. Воронин, Ю.В. Жнивцева, – М.: Экономика, 2012. – 535 с.
7. Неганова Л.М. Статистика: конспект лекций / Л.М. Неганова. – М.: Юрайт, 2007, – 220 с.
8. Кокрен У. Методы выборочного исследования, – М., 1976.
9. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З. Кучеренко. – М.: Гэотар-Медиа, 2007, учебное пособие для вузов.
10. Fernandez A.J. ; Perez-Gonzalez C.J. ; Kohansal A. Improved time-censored reliability test plans for k-out-of-n gamma systems //Journal of computational and applied mathematics, 2019, vol. 361, рр. 42-54 DOI: 10.1016/j.cam.2019.04.021
11. Gazi H.; Alhan C. Reliability of elastomeric-isolated buildings under historical earthquakes with/without forward-directivity effects //ENGINEERING STRUCTURES, 2019, vol. 195, рр. 490-507 DOI: 10.1016/j.engstruct.2019.05.081
12. Логанина В.И., Федосеев А.А. Статистические методы контроля и управления качеством продукции / В. И. Логанина, А. А. Федосеев. – Ростов-на-Дону, 2007. Сев. Серия «Высшее образование».
13. Логанина В.И. К вопросу о регулировании технологических процессов производства бетона // Известия высших учебных заведений. Строительство, № 3-4 (603-604), 2009, с. 42-45.
14. Логанина В.И., Хрусталева Б.Б., Учаева Т.В. Статистическое управление производством строительных изделий//Восточно-Европейский журнал передовых технологий, т. 1, № 3 (61), 2013, с. 65-67.
15. Логанина В.И., Круглова А.Н. Достоверность контроля качества строительных материалов и изделий // Вестник Белгородского государственного технологического университета им. В.Г. Шухова, №2, 2014, с. 16-18.
16. Логанина В.И., Учаева Т.В. К вопросу о системе контроля качества на предприятиях стройиндустрии // Региональная архитектура и строительство, №1, 2010, с. 31-33.