УДК 691.328
А.И. ШУМКОВ, канд. техн. наук
Ключевые слова: бетон, цемент, песок, щебень, гравий, макроструктура
Keywords: concrete, cement, sand, crushed stone, gravel, macrostructure
В современных условиях, когда расширяется ассортимент цементов, заполнителей и различных добавок, очевидна необходимость в корректировке методик расчета и подбора составов бетона для получения бетонных смесей, наиболее удобных для транспортирования и формования (укладки), а также создания наиболее рациональной макроструктуры бетона для тех или иных условий эксплуатации готовых изделий и конструкций.
Чтобы сэкономить цемент, практики часто стремятся составить смесь из песка и щебня (гравия) с наименьшей пустотностью. Она достигается при условии, кода зерна песка в уплотненном состоянии размещаются в пустотах щебня (гравия) также в уплотненном состоянии. В этом случае пустотность смеси обусловливается объемом пустот в песке.
Если этот объем пустот в песке только заполнить цементным тестом, то получаемая бетонная смесь будет слишком жесткая и неудобная для формования. Более того, смесь окажется недостаточно удобной для формования даже в том случае, если пустоты песка при его свободной насыпке (без встряхиваний) заполнить цементным тестом, а полученным раствором заполнить пустоты щебня или гравия также при их свободной насыпке.
Бетонная смесь становится достаточно удобоформуемой, а макроструктура бетона достаточно качественной, если объем цементного теста будет превышать объем пустот в смеси песка со щебнем или гравием при их свободной насыпке.
Практический опыт показывает, что насыпной объем израсходованного песка может быть и меньше объема пустот в израсходованном щебне или гравии, а также превышать этот объем, раздвигая их зерна. В этом случае объем цементного теста должен превосходить объем пустот в израсходованном песке и образовывать растворную часть бетона без пустот. Отношение объема раствора к объему пустот в щебне (гравии) называют коэффициентом раздвижки их зерен (α), который при избыточно повышенных расходах песка может оказаться таким, что теста не хватит, чтобы заполнить пустоты в песке, хотя зерна щебня (гравия) и будут раздвинуты.
В свое время в СССР был выполнен большой объем экспериментальных работ, обобщенных в [1]. В работе были показаны найденные экспериментальным путем оптимальные составы бетона в зависимости от расходов цемента и консистенции бетонной смеси. Бетонная смесь на цементе с плотностью зерен ρц =3,1 кг/л и с нормальной густотой цементного теста НГ =28%. Щебень с зернами 5…20 мм, плотностью ρщ=2,66 кг/л и насыпной плотностью ρ’щ=1,38 кг/л (при свободной насыпке). Песок крупнозернистый с модулем крупности МК=3, плотность зерен ρп =2,65 кг/л, насыпная плотность ρ’п =1,56 кг/л (также при свободной насыпке). Эти экспериментальные составы бетона показаны в таблице 1.
Таблица 1. Составы бетона на щебне 5…20 мм и крупнозернистом песке
| Показатели | Расход цемента, кг на 1 м3 бетона | ||||||
| 500 | 450 | 400 | 350 | 300 | 250 | 200 | |
| ОК, см | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| В/Ц | 0,48 | 0,52 | 0,58 | 0,65 | 0,75 | 0,90 | 1,125 |
| Расход песка, кг | 512 | 566 | 601 | 646 | 688 | 731 | 776 |
| ОК, см | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| В/Ц | 0,45 | 0,49 | 0,54 | 0,60 | 0,70 | 0,84 | 1,05 |
| Расход песка, кг | 516 | 562 | 604 | 650 | 690 | 734 | 780 |
| ОК, см | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| В/Ц | 0,42 | 0,46 | 0,50 | 0,56 | 0,65 | 0,78 | 0,98 |
| Расход песка, кг | 510 | 554 | 600 | 645 | 686 | 728 | 772 |
| ОК, см / Ж, сек | 2/5 | 2/5 | 2/5 | 2/5 | 2/5 | 2/5 | 2/5 |
| В/Ц | 0,38 | 0,41 | 0,45 | 0,50 | 0,59 | 0,71 | 0,88 |
| Расход песка, кг | 502 | 543 | 586 | 629 | 670 | 714 | 757 |
| Ж, сек | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| В/Ц | 0,35 | 0,38 | 0,41 | 0,46 | 0,53 | 0,64 | 0,80 |
| Расход песка, кг | 517 | 556 | 597 | 635 | 675 | 720 | 764 |
| Ж, сек | 17 | 17 | 17 | 17 | 17 | 17 | 17 |
| В/Ц | 0,31 | 0,33 | 0,36 | 0,40 | 0,46 | 0,55 | 0,70 |
| Расход песка, кг | 506 | 547 | 587 | 625 | 668 | 710 | 755 |
Из таблицы 1 видим, что при данном расходе цемента консистенция бетонной смеси и В/Ц в столбцах мало влияют на расход песка. Разница между максимальным и минимальным расходами песка составляет:
15 кг при Ц=500 кг в интервале В/Ц =0,31…0,48;
23 кг при Ц=450 кг в интервале В/Ц =0,33…0,52;
18 кг при Ц=400 кг в интервале В/Ц =0,36…0,58;
25 кг при Ц=350 кг в интервале В/Ц =0,40…0,65;
22 кг при Ц=300 кг в интервале В/Ц =0,46…0,75;
24 кг при Ц=250 кг в интервале В/Ц =0,55…0,90;
25 кг при Ц=200 кг в интервале В/Ц =0,70…1,125.
Таким незначительным влиянием практически можно пренебречь и принять максимальные величины расхода песка в каждом столбце таблицы 1 за величину, постоянную для указанных расходов цемента и интервалов В/Ц, независимую от консистенции бетонной смеси.
При этом в 7-ми столбцах данной таблицы выстраиваются два ряда:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Ц = | 500 | 450 | 400 | 350 | 300 | 250 | 200 |
| П = | 517 | 566 | 604 | 650 | 690 | 734 | 780 |
В столбцах этих двух рядов, применяя установленное в [1] (стр. 15) «постоянство абсолютного суммарного объема песка и цемента на данных материалах», получаем:
1-й. Ц1/ρц +П1/ρп=500/3,1+517/2,65 =356,4 (В/Ц =0,31…0,48);
2-й. Ц2/ρц +П2/ρп=450/3,1+566/2,65 =358,7 (В/Ц =0,33…0,52);
3-й. Ц3/ρц +П3/ρп=400/3,1+604/2,65 =356,9 (В/Ц =0,36…0,58);
4-й. Ц4/ρц +П4/ρп=350/3,1+650/2,65 =358,2 (В/Ц =0,40…0,65);
5-й. Ц5/ρц +П5/ρп=300/3,1+690/2,65 =357,1 (В/Ц =0,46…0,75);
6-й. Ц6/ρц +П6/ρп=250/3,1+734/2,65 =357,6 (В/Ц =0,55…0,90);
7-й. Ц7/ρц +П7/ρп=200/3,1+780/2,65 =358,8 (В/Ц =0,70…1,125).
Как видно, во всех столбцах получается практически близкий друг к другу результат, который можно выразить средней величиной для указанных в скобках величин В/Ц вне зависимости от консистенции бетонной смеси:
Ц/ρц +П/ρп = (356,4 + 358,7 + 356,9 + 358,2 + 357,1 + + 357,6 + 358,8)/7 =358
Таким образом, в бетоне на щебне находим для практического применения формулу расчета ориентировочного расхода песка с МК=3 в зависимости от расхода цемента в соответствующем ему интервале В/Ц:
П=ρп*(358-Ц/ρц) (1)
По мере уменьшения крупности песка его расход уменьшается. В [1] на стр. 11 показано, что с переходом от песка с МК=3 к песку с МК=0,9 его расход уменьшается на 10…14% в интервале расхода цемента 200…500 кг. В среднем можно принять 12% для любого расхода цемента в этом интервале и выразить коэффициент уменьшения расхода песка (кмк) в зависимости от МК линейным уравнением по следующим двум рядам:
МК=0,9 3,0;
кмк =0, 88 1,0.
Моделирование по этим рядам привело к формуле:
кмк=0,83+0,057*MK. (2)
Тогда формула (1) примет вид:
П =ρп*(358- Ц/ρц)* кмк (3)
Если применяется гравий, то там же показано, что расход песка уменьшается на 9…11% и, следовательно, рассчитанный по формуле (3) расход песка уменьшается в среднем на 10%.
Формула (3) позволяет отказаться от нахождения расхода песка путем назначения различных коэффициентов по эмпирическим таблицам накопленного опыта и перейти к назначению непосредственно расхода песка по заданным показателям В/Ц и расхода воды. Тем не менее надо контролировать все применяемые на практике коэффициенты, такие как раздвижки зерен щебня (гравия) раствором (α) или заполнения пустот щебня (гравия) песком (k), а также раздвижки зерен смеси песка с гравием (щебнем) цементным тестом (αц), объемную долю песка в смеси песка с гравием или щебнем (r %), так как они несут информацию о структуре и свойствах бетонной смеси и готового бетона, и сравнивать табличные данные с фактически полученными. При этом добавить к ним еще один коэффициент: раздвижки зерен песка цементным тестом α’ц., так как он формирует макроструктуру и прочность растворной части бетона.
Раздвижка зерен щебня или гравия раствором уменьшает число точек контакта зерен и делает каркас из них более ажурным и менее устойчивым к восприятию нагрузок.
При переходе от более компактного каркаса зерен при их насыпке в измерительный сосуд со встряхиванием к менее компактному каркасу зерен при их насыпке без встряхивания пустотность каркаса возрастает. И если при этом пустотность возросла, например, с 42% до 50%, то коэффициент раздвижки зерен α=50/42=1,19. При раздвижке раствором зерен щебня или гравия от их рыхло-насыпного состояния пустотность каркаса увеличивается, например, при α =1,25 до 50*1,25 =62,5%, а при α =1,4 до 50*1,4=70%. Если вести отсчет от уплотненного состояния зерен щебня или гравия, то α=62,5/42=1,49 и 70/42 =1,67. В этом последнем случае бетонная смесь расслаивается, а при транспортировке и укладке вибрированием или иным способом зерна щебня (гравия), а также песка, стремясь в совокупности к наиболее компактной упаковке, выдавливают «лишнее» цементное тесто в виде воды, которая скапливается на поверхности уложенного бетона. Вместе с водой вымываются изнутри и наиболее мелкие, т.е. наиболее активные к гидратации частицы цемента, чего допускать нельзя.
Таким образом, в зависимости от свойств применяемых крупных (К) и мелких (М) заполнителей коэффициент α при отсчете от рыхло-насыпного состояния зерен должен быть ограничен определенной величиной порядка: 1,40…1,45 – для бетонов на щебне и 1,45…1,50 – для бетонов на гравии. Недостающую подвижность бетонных смесей следует повышать введением в них пластифицирующих и воздухововлекающих добавок.
При заданном В/Ц признаки расслоения бетонной смеси на щебне появляются уже при α=1,35, а на гравии при α=1,4, усиливаясь по мере увеличения α. Предельные величины α могут быть найдены только экспериментально в зависимости от свойств конкретно применяемых материалов, водоцементного отношения (В/Ц) и расхода цемента (Ц).
Если зерна заполнителей моделировать шарами, то теоретически наибольшая пустотность упаковки шаров одинакового диаметра независимо от его размера достигается в тетраэдрической решетке и составляет 66%, образуя каркас, в котором каждый шар контактирует с четырьмя соседними шарами. Наименьшая пустотность шаров формируется в гранецентрированной кубической либо в гексагональной решетках и равна 26%, образуя каркас, в котором каждый шар контактирует с двенадцатью шарами-соседями [2] и [3]. Однако теоретическую пустотность 26% практически получать не удается. Мелкие шары показывают обычно более высокую пустотность, чем крупные, и она может доходить до 47% [4] при их свободной насыпке в измерительный сосуд (без встряхиваний).
При раздвижке зерен песка цементным тестом в растворной части бетона происходят те же явления, что и при раздвижке зерен щебня (гравия) раствором. Разница в том, что часть цементного теста уходит на обмазку зерен щебня (гравия) и эта «прилипшая» к их поверхности часть не участвует в раздвижке зерен песка, но присутствует в раздвижке зерен смеси песка со щебнем (гравием). Зерна наиболее крупных фракций песка, оставаясь в растворной части, встраиваются в каркас из щебня или гравия, увеличивая жесткость и несущую способность получаемого скелета.
В таблице 2 показаны ориентировочные расходы воды (В, л) на 1 м3 бетона для наиболее употребительных марок бетонной смеси при наибольшей крупности зерен щебня и гравия НК=10, 20, 40 и 70 мм (по накопленному практическому опыту).
Таблица 2
| Характеристика бетонной смеси | Ориентировочные расходы воды, л на 1 м3 бетона при наибольшей крупности заполнителя, НК, мм | |||||||||
| Марка | ОК, см | Ж, сек | 10 | 20 | 40 | 70 | ||||
| Грв. | Щб. | Грв. | Щб. | Грв. | Щб. | Грв. | Щб. | |||
| Ж 3 | — | 30-21 | 165 | 175 | 155 | 165 | 140 | 150 | 135 | 145 |
| Ж 2 | — | 20-11 | 175 | 185 | 165 | 175 | 150 | 160 | 145 | 155 |
| Ж 1 | — | 10-5 | 185 | 195 | 175 | 185 | 160 | 170 | 155 | 165 |
| П 1 | 1-4 | 4-1 | 195 | 205 | 185 | 195 | 170 | 180 | 165 | 175 |
| П 2 | 5-9 | — | 205 | 215 | 195 | 205 | 180 | 190 | 175 | 185 |
| П 3 | 10-15 | — | 215 | 225 | 205 | 215 | 190 | 200 | 185 | 195 |
Пример. Готовится бетонная смесь марки П1 с требуемыми показателями осадки конуса ОК=1…4 см и В/Ц=0,55 на гранитном щебне с зернами 5…20 мм и мелком песке.
Плотность зерен щебня ρщ =2,71 кг/л, насыпная плотность ρ’щ =1,44 кг/л, пустотность Пщ=0,47. Песок с модулем крупности МК=1,89, плотность зерен ρпс=2,7 кг/л, насыпная плотность ρ’пс =1,38 кг/л, пустотность Ппс =0,49. При рассеве песка получены частные остатки на ситах: 2,5 мм – 4,9%; 1,25 мм – 7,6%; 0,63 – 10,4%; 0,315 – 39,1%; 0,16 – 24,7%; менее 0,16 – 13,3%.
По таблице 2 расход воды В=195 л.
Расход цемента по формуле:
Ц=В/(В/Ц) (4)
Ц=195/0,55=355 кг, а песка по формуле (3) с учетом, что кмк=0,83+ 0,057*MK=0,83+0,057*1,89=0,938, П=2,7*(358-355/3,1)*0,938=617 кг.
Расход щебня по формуле:
Щ=ρщ*(1000-Ц/ρц-П/ρпс-В-VV) (5)
Щ=2,71*(1000-355/3,1-617/2,7-190-0)=1252 кг (пренебрегая воздухововлечением VV, если оно не превышает 20 л. в 1 м3 бетона).
Находим фактический коэффициент α по формуле:
α=(Ц/ρц +В+П/ρпс )/(Щ *Пщ/ρ’щ) (6)
α=(355/3,1+195+617/2,7)/(1252*0,47/1,44)=1,32
Фактическая осадка конуса бетонной смеси ОК =1 см.
В получаемых по формулам (3, 4, 5) составах бетонных смесей нельзя найти фактический коэффициент α’ц раздвижки зерен песка цементным тестом, так как неизвестно, сколько теста, не участвующего в раздвижке зерен песка, «прилипает» к поверхности зерен щебня при их обмазке.
Количество «прилипшего» теста к поверхности зерен щебня или гравия зависит от их водоудерживающей способности, которую характеризуют по ГОСТ 8269-76 коэффициентом смачивания (ксм) и от вязкости цементного теста, на которую влияет водоцементное отношение.
ГОСТ 8269-76 регламентирует погружать навеску высушенных зерен щебня (гравия) в воду на 30 мин., извлекать, встряхивать на сите с мелкой сеткой и обтирать зерна мягкой тканью. На основе испытаний по этому ГОСТу были рекомендации учитывать в расчетах получаемые величины ксм =1…2% от массы щебня (гравия) [4] (стр. 44), которые, однако, на практике не нашли применения.
Мы изменили регламент ГОСТ 8269-76 и зерна щебня (гравия) не протирали мягкой тканью, а протирали наружную поверхность сетки, полагая, что получим при этом не коэффициент смачивания, а водоудерживающую способность зерен щебня (гравия) Wуд,%. В разных щебнях она составляла 2…3%, у гравия 1…2%.
Зная Wуд, можно вычислить – сколько цементного теста «прилипает» к поверхности зерен щебня (гравия) при их обмазке. Покажем это на приведенном примере.
Количество воды, удерживаемой на поверхности зерен щебня Вщ:
Вщ =Щ* Wуд/100 (7)
При Wуд =2,45% Вщ =1252* 2,45/100 =30,7 л
Количество цемента (Цщ, кг), необходимое для Вщ при заданном В/Ц:
Цщ =Вщ /(В/Ц) (8)
При В/Ц =0,55 Цщ =30,7/0,55 =55,8 кг.
Цементное тесто, прилипшее к поверхности зерен щебня (ЦТщ):
ЦТщ=Цщ/ρц + Вщ (9)
ЦТщ =55,8/3,1 + 30,7 =48,7 л.
А так как общее ЦТ= Ц/ρц+В=355/3,1+195=309,5 л, то на раздвижку зерен песка остается 309,5-48,7=260,8 л.
Коэффициент раздвижки зерен песка цементным тестом:
α’ц=(ЦТ-ЦТщ) /(П*Ппс/ρ’пс) (10).
α’ц=(309,5-48,7)/(617*0,49/1,38) =1,19
Формулы (3)…(10) были применены для создания компьютерной программы в системе Матлаб.
Чтобы повысить число точек контакта зерен заполнителей и несущую способность образуемого при α=1,32 нового скелета из зерен щебня и крупных фракций песка, необходимо, как показали исследования, увеличить в мелком песке количество зерен крупных фракций. Для этого ситом 0,16 мм отсеяли фракцию менее 0,16 мм и получили следующие новые частные остатки на ситах: 2,5 мм – 5,6%; 1,25 мм – 10,1%; 0,63 – 12%; 0,315 – 45,1%; 0,16 – 28,5%. Модуль крупности песка повысился с 1,89 до 2,18. Также повысилась и насыпая плотность с 1,38 до 1,40 кг/л. Пересчет состава бетонной смеси на этом «новом» песке показал, что расходы цемента (355 кг) и воды (195 л) не изменились, расход песка увеличился с 617 до 628 кг, а щебня – уменьшился с 1252 до 1242 кг. При этом все коэффициенты увеличились: r, % – от 33,1 до 33,7; k – от 1,097 до 1,11; αц – от 1,416 до 1,433; α’ц – от 1,19 до 1,21; α – от 1,32 до 1,34. Фактическая осадка конуса (ОК) увеличилась с 1 до 2,5 см.
На примененном в экспериментальных работах цементе марки 42,5 средняя прочность бетона при сжатии повысилась с 35,4 МПа до 39,2 МПа. В российской практике при расчете составов бетона чаще всего применяют коэффициент раздвижки зерен щебня (гравия) раствором (α). Поэтому в Матлабе была создана показанная на рисунке номограмма, выражающая зависимость коэффициента α от В/Ц и консистенции бетонной смеси соединением прямыми линиями точек, полученных по экспериментальным данным составов, приведенных в [1].
С вопросами по созданию и установке на компьютер программы проектирования номинальных составов и макроструктуры бетона с В/Ц=0,35…1,0 и расходами цемента 200…500 кг на 1 м3 бетона обращаться по адресу электронной почты: shumkov-a@ya.ru.
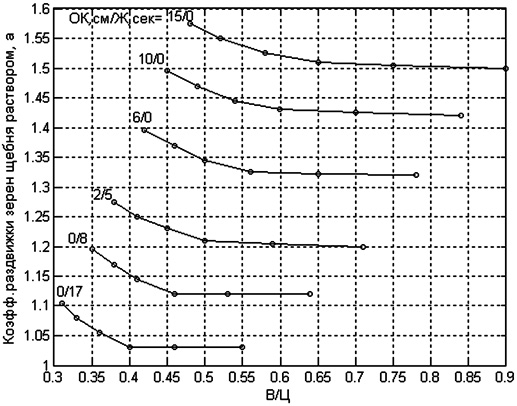
Зависимость коэффициента α от пластичности бетонной смеси по осадке конуса на стандартном конусе и от жесткости на стандартном вискозиметре (песок с МК=3, щебень 5…20 мм, цемент с НГ=28%).
Библиографический список
1. Сизов В.П. Проектирование составов тяжелого бетона, – Москва: Стройиздат, 1979, 149 с., с. 11, 12, 15, 18, 19, 20, 21.
2. Васильев Д.М. Физическая кристаллография, «Металлургия», 1981, 243 с., с. 223.
3. Шумков А.И. Теоретические и практические основы формирования макроструктуры тяжелого бетона // Технологии бетонов,
№9-10, 2010, с. 48-49,
4. Баженов Ю.М. Технология бетона, Ассоциация строительных вузов, – Москва, 2002, 499 с., с. 31, 44.