УДК 691(075.3)

Л.И. ДВОРКИН, доктор техн. наук, профессор, О.М. БОРДЮЖЕНКО, канд. техн. наук, доцент, Н.М. СКРЫПНЫК, аспирант, Национальный университет водного хозяйства и природопользования, г. Ровно, Украина

Ключевые слова: фибробетон, фибра, суперпластификатор, расчет состава, критерий оптимальности
Keywords: fibered concrete, fiber, superplasticizer, composition design, optimality criterion

На основе экспериментально-статистических моделей прочности и расхода суперпластификатора предложена методика проектирования составов фибробетонов, позволяющая получать расчетные значения содержания компонентов смеси, необходимых для обеспечения нормированного комплекса их строительно-технических свойств. Разработанная методика позволяет учитывать конкретные особенности исследуемых материалов и оптимизировать состав фибробетона по определенному критерию, например критерию минимальной стоимости.

При проектировании составов бетона основными критериями их оптимизации обычно выступают минимальный расход цемента или минимально возможная стоимость бетона. Для обычных бетонов эти критерии, как правило, совпадают. При этом обязательным является обеспечение комплекса нормируемых свойств бетонной смеси и бетона.

Современные бетоны являются многокомпонентными системами, стоимость отдельных компонентов которых может приближаться или превышать стоимость цемента. К таким бетонам отнесят фибробетоны. Они отличаются наличием трех компонентов (цемента, фибры и добавки-пластификатора), содержание которых может изменяться в широком диапазоне и оказывать основное влияние на суммарную стоимость фибробетона.

Задача минимизации стоимости фибробетона при обеспечении комплекса заданных свойств существенно усложняется. Для ее решения целесообразно применять методы математического программирования [1-2].

В данной статье приведена методика и примеры решения такой задачи с использованием экспериментально-статистических моделей прочности при сжатии и при изгибе фибробетона в разном возрасте, а также модели необходимой добавки-суперпластификатора для обеспечения заданных показателей бетона и бетонной смеси1.

Таблица 1. Условия планирования эксперимента

№	Факторы		Уровни варьирования			Интервал
	Код	Натуральный вид	-1	0	+1
1	Х1	Расход цемента, кг/м3 (Ц)	450	500	550	50
2	Х2	В/Ц	0,3	0,35	0,4	0,05
3	Х3	Расход фибры, кг/м3 (Ф)	80	100	120	20

Постановку задачи нахождения оптимального состава фибробетона с заданными показателями качества можно сформулировать следующим образом: найти значения факторов состава фибробетона x1…xn, позволяющие минимизировать стоимость фибробетона:

СФБ = Сц⋅Ц + СД⋅Д + СФ⋅Ф → min (1)

При условии обеспечения требуемых показателей качества

П1 ≥ f (x1, x2,…, xn); (2)

П2 ≥ f (x1, x2,…, xn);

……………………

Пm ≥ f (x1, x2,…, xn) (3)

при x1… xn ∈ [a…b],

где Cц, CД, CФ – соответственно стоимость цемента, добавки-модификатора (суперпластификатора, активной минеральной добавки и т.д.) и фибры, у.е./кг;

Ц, Д, Ф – соответственно расход цемента, добавки-модификатора и фибры, кг/м³ фибробетона;

П1…Пm – заданные показатели качества фибробетона;

x1…xn – факторы состава;

a, b – ограничения на возможные значения факторов.

Для определения параметров составов сталефибробетонов была реализована серия экспериментов, алгоритмизированных в соответствии с трехфакторным планом эксперимента второго порядка (типа В3) [3] при условиях планирования, приведенных в табл. 1. В качестве исходных компонентов бетонной смеси использовали цемент ПЦ-II М500 АО «Волынь-цемент», заполнитель в виде фракционированной смеси из кварцевого песка (0,16…2 мм) и гранитного щебня (2…5 мм) в соотношении 0,45/0,55. В бетонные смеси вводили суперпластификатор поликарбоксилатного типа Melflux 2651f в количестве, обеспечивающем подвижность смеси в пределах 15…18 см. Использовали волнистую фибру из низкоуглеродистой стали типа Fibax Ф1 60/1 (длина 60,0 ± 6,0 мм, диаметр 1,0 ± 0,1 мм) [4].

Результаты экспериментов приведены в табл. 2.

Таблица 2. Экспериментальные результаты

№ точек плана	Кодированные значения факторов			Расход компонентов, кг/м3				В/Ц	Суперпластификатор, %	Прочность, МПа
										при сжатии Rсж 28	при изгибе Rизг 28
	Х1	Х2	Х3	цемент	заполнитель	вода	фибра
1	1	1	1	550	1627	220	120	0,4	0,2	67,2	13,84
2	1	1	-1	550	1627	220	80	0,4	0,1	66,6	9,08
3	1	-1	1	550	1776	165	120	0,3	1,1	96	19,92
4	1	-1	-1	550	1776	165	80	0,3	0,8	95,2	15,23
5	-1	1	1	450	1822	180	120	0,4	0,4	57,3	14,9
6	-1	1	-1	450	1822	180	80	0,4	0,2	56,9	9,59
7	-1	-1	1	450	1944	135	120	0,3	1,3	83,9	17,06
8	-1	-1	-1	450	1944	135	80	0,3	1	83,3	11,82
9	1	0	0	550	1702	193	100	0,35	0,45	79,7	18,13
10	-1	0	0	450	1883	158	100	0,35	0,27	75,8	16,95
11	0	1	0	500	1724	200	100	0,4	0,3	65,3	15,49
12	0	-1	0	500	1860	150	100	0,3	0,5	92,4	19,64
13	0	0	1	500	1792	175	120	0,35	0,3	79	15,67
14	0	0	-1	500	1792	175	80	0,35	0,1	77,5	10,67
15	0	0	0	500	1792	175	100	0,35	0,2	78,3	17,05
16	0	0	0	500	1792	175	100	0,35	0,2	78,1	17,17
17	0	0	0	500	1792	175	100	0,35	0,2	77,9	17,25

После проведения обработки и статистического анализа экспериментальных данных получены математические модели прочности при сжатии и растяжении при изгибе в возрасте 28 суток стандартных бетонных кубов в виде полиномиальных уравнений регрессии (4-5). Адекватность полученных моделей подтверждена соответствующими значениями критерия Фишера [3].

Модели прочности, представленные в кодированном виде, МПа:

– при сжатии: Rсж28=78,9+4,8·Х1-13,8·Х2+0,4·Х3-1,53·Х12-0,43·Х22-Х32-0,5·Х1·Х2 (4)

– растяжении при изгибе:

Rизг28=17,2+0,59·Х1-2,08·Х2+2,5·Х3+0,36·Х12+0,38·Х22-4,01Х32-0,98·Х1·Х2-0,14·Х1·Х3 (5)

Для определения расхода суперпластификатора Melflux 2651f получена следующая математическая модель, % от массы цемента:

СП’=0,29+0,095·Х1-0,35·Х2+0,11·Х3-0,05·Х12+0,23·Х22+0,03·Х32-0,04·Х2·Х3. (6)

Перевод значений параметров состава фибробетонных бетонной смеси в кодированный вид проводился с помощью зависимостей:

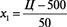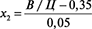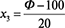; ; . (7)

Полученные полиномиальные модели (4-6) позволяют решать ряд практических задач. Согласно В.А. Вознесенскому [2], известно 10 типов задач, которые могут быть решены индивидуально или совместно на основе таких моделей. Это интерполяционные, экстраполяционные задачи, задачи достижения минимального или максимального значения выходного параметра и др.

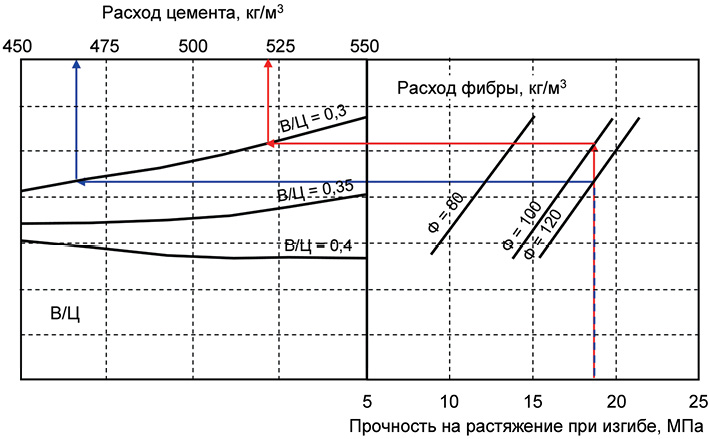
Задачи минимизации ресурсов и управления при фиксированном исходном параметре могут решаться аналитическим и номографическим способами. Задача управления составом заключается в определении комбинаций факторов, обеспечивающих заданные показатели выходного параметра. Для этого из полученного уравнения регрессии – например, прочности на растяжение при изгибе (2) – выбирают один из факторов, скажем, расход цемента. В результате решения уравнения регрессии относительно этого фактора определяют необходимое его значение, обеспечивающее при изменении других факторов заданное значение выходного параметра. На рис. 1 приведена номограмма для определения расхода цемента при заданной прочности фибробетона на растяжение при изгибе.

Для фибробетонов, как уже отмечалось ранее, кроме цемента, на стоимость существенно влияет расход фибры. Например, на рис. 1 рассмотрен случай, когда необходимую прочность на растяжение при изгибе 18 МПа можно достичь при одном и том же В/Ц=0,3, но при различных расходах фибры (100 и 120 кг) и цемента (522 и 468 кг). Если учесть необходимость дополнительного определения расхода суперпластификатора, который влияет как на свойст­ва бетона, так и на его стоимость, а также обеспечения комплекса нормируемых свойств, например прочности на растяжение при изгибе и при сжатии, то становится понятным, что задачу оптимизации состава фибробетона решить номографическим способом практически невозможно.

Для того чтобы рассчитать оптимальный состав фибробетона, необходимо решить задачу математического программирования. В данном случае задачу оптимизации можно сформулировать следующим образом: найти состав фибробетонной смеси заданной подвижности с минимальной суммарной стоимостью, позволяющий обеспечить необходимую прочность бетона при сжатии и растяжении при изгибе в возрасте 28 суток в пределах допустимых значений влияющих факторов.

Одним из рациональных способов решения такой задачи является использование программной среды Microsoft Excel, в частности ее приложения «Поиск решения». Это приложение предназначено для поиска решения уравнений и задач оптимизации.

Последовательность расчета следующая. Подставляем в модели (4) и (5) значения прочности, которые должны обеспечиваться, а в уравнение (1) – значения стоимости компонентов фибробетона. В уравнении 3 учитываем необходимые ограничения значений факторов (в кодированном виде от -1 до 1). Программа в результате перебора (итераций) различных комбинаций факторов обеспечивает значения прочности не менее заданных и находит значения факторов состава согласно уравнениям (4) и (5), минимизируя при этом функцию (1). Для установления стоимости фибробетона при выполненных итерациях параллельно определяется необходимое содержание суперпластификатора из уравнения (6) при найденных комбинациях факторов х1 … х3.

Результатом таких итераций является определение оптимальных значений расхода цемента, фибры, В/Ц и суперпластификатора. Расход воды можно рассчитать по найденному В/Ц и расходу цемента:

В=Ц⋅В/Ц (8)

Значения расхода заполнителя находим по методу абсолютных объемов:

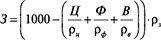, (9)

где ρц, ρф, ρв, и ρз – соответственно истинные плотности цемента, фибры, воды и заполнителя.

Пример 1. Определить состав мелкозернистого фибробетона с прочностью при сжатии 70 МПа и растяжении при изгибе 15 МПа в возрасте 28 суток с подвижностью смеси 15 см, используя экспериментально-статистические модели (4-6). Принимаем стоимости основных компонентов фибробетона следующими: у.е./кг: Сц =0,1; ССП=9; СФ =1,8. Материалы: портландцемент М500, мелкий заполнитель с модулем крупности 3,5 среднего качества и плотностью ρз=2,65 кг/л. Предполагается использование суперпластификатора Melflux 2651 f.

1. Подставляя значение необходимой прочности при сжатии и изгибе в уравнения (4) и (5), получим функции ограничений (2) задачи:

Rсж28 : 78,9+4,8·Х1-13,8·Х2+0,4·Х3-1,53·Х12-0,43·Х22-Х32-0,5·Х1·Х2+0,05·Х1·Х3-0,05·Х2·Х3 ≥ 70; (10)

Rизг28 :17,2+0,59·Х1-2,08·Х2+2,5·Х3+0,36·Х12-+0,38·Х22-4,01Х32-0,98·Х1·Х2-0,14·Х1·Х3+0,02·Х2·Х3 ≥ 15. (11)

2. В уравнение (1) подставляем значения стоимости компонентов фибробетона, а также задаем ограничения значений принятых факторов состава: от -1 до 1 (в кодированном виде).

3. С помощью программного приложения «Поиск решения» находим кодированные значения факторов, удовлетворяющие принятым ограничениям и минимизирующие стоимость фибробетона:

x1 =-0,039; x2 =0,13; x3 =-0,446

Найденные значения факторов обеспечивают установленные ограничения (10-11): Rсж28 =76,6 МПа; Rизг28=15 МПа.

4. Значения факторов состава в натуральном виде определяем по формулам (7):

Ц=50∙х1 + 500=50∙(-0,026)+500=498,1 кг/м³

В/Ц=0,05∙х2+0,35=0,05∙0,13+0,35=0,356

Ф=20∙х3+100=20∙(-0,446)+100=91,1 кг/м³

5. Расход суперпластификатора из уравнения (6):

– в % от массы цемента:

СП’=0,29+0,095·Х1-0,35·Х2+0,11·Х3-0,05·Х12+0,23·Х22+0,03·Х32-0,04·Х2·Х3 =0,21%

– по массе:

СП=СП’∙Ц/100=0,21∙498,1/100=1,046 кг/м³.

6. Значение минимально возможной стоимости 1 м3 фибробетона без учета стоимости заполнителя и воды (1):

СФБ=0,1⋅498,1+9⋅1,045+1,8⋅91,1=222,3 у.е.

7. Расход воды (8):

В=498,1⋅0,356=177,5 л.

8. Расход заполнителя (9):

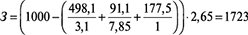кг.

Окончательный состав фибробетонной смеси, кг/м³:

Ц=498; В=178; З=1723; Ф=91; СП=1,05.

На этапе формулировки задачи определения оптимального состава фибробетона необходимо корректно задаваться желаемыми значениями показателей его качества. Очевидно, что эти значения должны находиться в диапазоне минимально и максимально возможных в соответствии с используемыми полиномиальными моделями. Эти значения можно достаточно легко найти, применяя программное приложение «Поиск решения». Так, для рассматриваемого примера 1 предельные значения прочности в пределах области варьирования факторов будут следующими:

Rсж28 (min)=58,2 МПа; Rсж28 (max)=96,1 МПа;

Rизг28 (min)=8,9 МПа; Rизг28 (max) =21,9 МПа.

Возможен также некоторый выход за предельные границы значений исходных параметров. В этом случае наряду с задачей оптимизации решается также экстраполяционная задача, позволяющая принимать значения факторов за пределами области варьирования (например, х1…х3=1,1; 1,2; 1,3). Однако необходимо иметь в виду, что экстраполяция может быть связана с определенными ошибками, и эти ошибки становятся более ощутимыми, чем дальше выход за пределы области варьирования. Экстраполяция возможна, если по результатам исследований не возникает сомнений, что за пределами области варьирования факторов характер функции остается неизменным.

Рассмотрим еще один пример расчета, включающий фиксацию одного из факторов на определенном уровне.

Пример 2. Условия задачи полностью соответствуют исходным данным примера 1, но дополнительно необходимо ограничить расход фибры минимально возможным значением, т.е. Ф=80 кг/м³.

1. Функции ограничений задачи аналогичны п. 1 (пример 1).

2. Задаем ограничения значений факторов: x1=x2=-1 … 1; x3=-1 (в кодированном виде). Значение стоимости компонентов фибробетона подставляем в уравнение (1).

3. С помощью программного приложения «Поиск решения» находим значения факторов, удовлетворяющие ограничениям задачи и минимизирующие стоимость фибробетона:

x1 =0,914; x2 =-0,992; x3 =-1.

При найденных значениях факторов по уравнениям (4-5) Rизг28=15 МПа и Rсж28=94,3 МПа.

4. Значения факторов в натуральном виде определяем по формулам (7):

Ц=50∙х1+500=50∙0,914+500=545,7 кг;

В/Ц=0,05∙х2+0,35=0,05∙(-0,992)+0,35=0,3;

Ф=20∙х3+100=20∙(-1)+100=80 кг.

5. Расход суперпластификатора (6):

– в % от массы цемента: СП’=0,854%;

– по массе: СП=СП’∙Ц/100=0,854∙545,7/100=4,66 кг.

6. Значение минимально возможной стоимости 1 м³ фибробетона без учета стоимости заполнителя и воды:

СФБ=0,1⋅545,7+9⋅4,66+1,8⋅80=240,5 у.е.

7. Расход воды (8):

В=545,7⋅0,3=163,9 л.

8. Расход заполнителя (9):

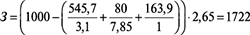кг.

Состав фибробетонной смеси, кг/м³:

Ц=546; В=164; З=1722; Ф=80; СП=4,66.

Анализируя полученный состав и сравнивая его с примером 1, стоит отметить, что при ограничении расхода фибры становится сложнее достичь заданной прочности на растяжение при изгибе. По этой причине необходимо идти на некоторый перерасход цемента и суперпластификатора, что приводит к образованию существенного запаса по прочности при сжатии – 94,3 МПа вместо минимально необходимого значения 70 МПа.

Выводы:

1. Предложенный метод расчета состава фибробетона позволяет учитывать конкретные особенности исследуемых материалов и достаточно легко оптимизировать состав по необходимому критерию, например по критерию минимальной стоимости.

2. К преимуществам метода следует отнести возможность введения определенного количества ограничений, что позволяет одновременно обеспечивать значительное количество показателей качества при их заданных значениях.

Библиографический список

1. Dvorkin L., Dvorkin O., Ribakov Y. Multi-Parametric Concrete Compositions Design. – Nova Science Publishers, – New York, 2013, – 223 p.
2. Вознесенский В.А., Ляшенко Т.В., Огарков Б.Л. Численные методы решения строительно-технологических задач на ЭВМ. – К.: Вища шк., 1989, – 328 с.
3. Dvorkin L., Dvorkin O., Ribakov Y. Mathematical experiments planning in concrete technology. – Nova Science Publishers, – New York, 2012, – 173 p.
4. Дворкин Л.И. и др. Высокопрочные быстротвердеющие бетоны и фибробетоны. – Ровно: НУВХП, 2017, – 331 с. (укр.).

---