И.А. ЕМЕЛЬЯНОВА, доктор техн. наук, профессор; А.А. ЗАДОРОЖНЫЙ, канд. техн. наук, доцент, Харьковский национальный университет строительства и архитектуры; Ю.В. ЧОВНЮК, канд. техн. наук, доцент, Национальный университет биоресурсов и природопользования Украины, г. Киев; Н.А. МЕЛЕНЦОВ, главный инженер ООО «Стальконструкция», г. Харьков
В статье рассмотрены условия транспортирования бетонных смесей по эластичным трубопроводам при работе как двухпоршневых растворобетононасосов, так и в ряде случаев бетононасосов.
Проанализирована подача бетонной смеси эластичными трубопроводами (шлангами) при допустимой скорости волны давления в трубопроводе и создании условий стабильной подачи смеси при отсутствии автоколебаний.
Двухпоршневые растворобетононасосы различных конструктивных решений независимо от выполнения работ как при чистом транспортировании бетонных смесей, так и при выполнении торкрет-работ [1, 2] оснащаются гибкими эластичными трубопроводами (шлангами). В связи с этим требуется изучить возможности таких трубопроводов, которые обеспечивают стабильную равномерную подачу смесей либо к потребителю, либо к рабочему соплу при минимальных затратах энергии.
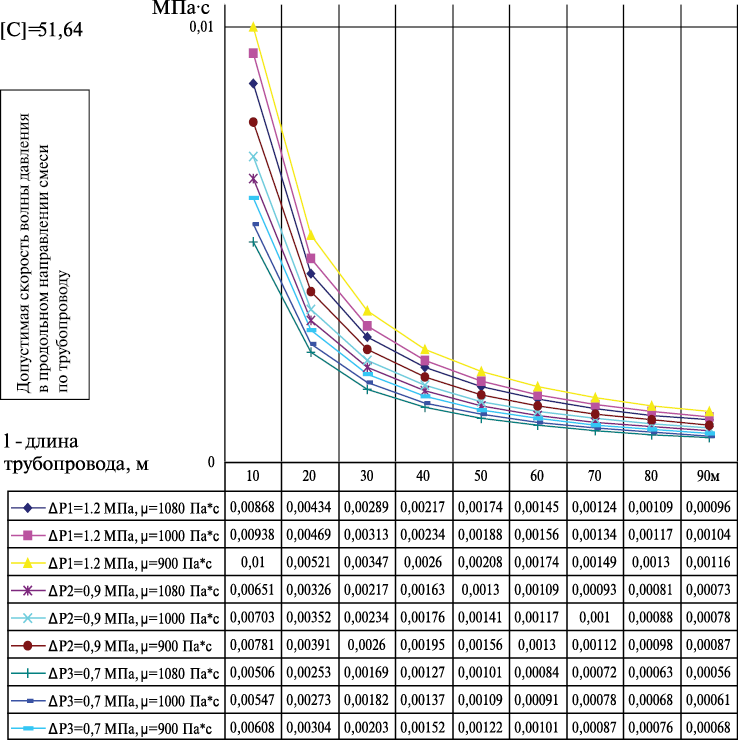
Примечание: подвижность смеси П1=4,5…6 см, вязкость μ1= 1080 Па·с; μ2= 1000 Па·с; μ3=900 Па·с
В работе Волобуева А.Н. и Толстоногова А.П. [3] показано, что векторная форма уравнения импульса справедлива как для потока смеси, транспортируемой по жесткому трубопроводу, так и по эластичному трубопроводу, и имеет вид:
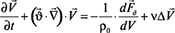 , (1)
, (1)
где 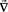 – оператор Гамильтона; Δ – оператор Лапласа; ρ0 – средняя плотность бетонной смеси; dV – дифференциал ее объема; v – кинематическая вязкость бетонной смеси, t – время, за которое смесь проходит всю длину трубопровода;
– оператор Гамильтона; Δ – оператор Лапласа; ρ0 – средняя плотность бетонной смеси; dV – дифференциал ее объема; v – кинематическая вязкость бетонной смеси, t – время, за которое смесь проходит всю длину трубопровода; 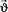 – скорость движения смеси;
– скорость движения смеси; 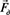 – сила, движущая поток смеси по трубопроводу.
– сила, движущая поток смеси по трубопроводу.
Согласно результатам исследований тех же авторов [4], слагаемое 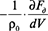 , определяющее движущую силу потока смеси в эластичном трубопроводе, в проекции на ось Ох можно представить как:
, определяющее движущую силу потока смеси в эластичном трубопроводе, в проекции на ось Ох можно представить как:
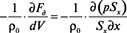 , (2)
, (2)
где p – давление, обеспечивающее движение смеси по трубопроводу; Sx – площадь поперечного сечения трубопровода, являющаяся функцией координаты х.
Уравнение (2) справедливо при относительно небольшой деформации внутренних стенок эластичного трубопровода.
Для бетонной смеси определенной вязкости, транспортируемой по эластичному трубопроводу, на основании данных [2] имеем:
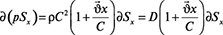 , (3)
, (3)
где 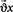 – средняя скорость движения смеси по сечению трубопровода вдоль оси Ox; D = ρC2 [4] – коэффициент упругости стенок трубопровода;
– средняя скорость движения смеси по сечению трубопровода вдоль оси Ox; D = ρC2 [4] – коэффициент упругости стенок трубопровода;
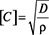 , (4)
, (4)
где  – допустимая скорость волны давления в трубопроводе в продольном направлении движении смеси; D ≡ E, где E – модуль упругости трубопровода (шланга), по которому транспортируется смесь; ρ – плотность материала шланга.
– допустимая скорость волны давления в трубопроводе в продольном направлении движении смеси; D ≡ E, где E – модуль упругости трубопровода (шланга), по которому транспортируется смесь; ρ – плотность материала шланга.
В таком случае уравнение импульса для потока смеси в эластичном трубопроводе имеет вид:
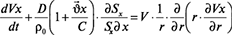 , (5)
, (5)
где r – текущий радиус трубопровода.
При использовании закона Гука для эластичного трубопровода 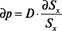 [5], а уравнение импульса может быть представлено как:
[5], а уравнение импульса может быть представлено как:
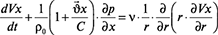 . (6)
. (6)
В данном случае перед относительной деформацией площади сечения трубопровода 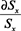 следует брать знак плюс. Это связано с тем, что с повышением давления ρ, при котором транспортируется смесь по эластичному трубопроводу, увеличивается и площадь его поперечного сечения.
следует брать знак плюс. Это связано с тем, что с повышением давления ρ, при котором транспортируется смесь по эластичному трубопроводу, увеличивается и площадь его поперечного сечения.
При постоянном перепаде давления 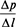 на длине трубопровода Δl после двойного интегрирования уравнения (5) скорость движения смеси Vx определяется как:
на длине трубопровода Δl после двойного интегрирования уравнения (5) скорость движения смеси Vx определяется как:
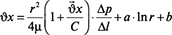 . (7)
. (7)
Постоянная а=0, поскольку на оси трубы скорость смеси конечна. Постоянная b находится из условия 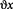 = 0 при r = Rmp, где Rmp – радиус трубопровода, следовательно:
= 0 при r = Rmp, где Rmp – радиус трубопровода, следовательно:
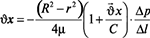 . (8)
. (8)
Знак минус перед выражением справа в (7) показывает, что 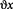 > 0 при
> 0 при 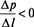 .
.
Расход бетонной смеси определяется согласно формуле:
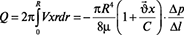 . (9)
. (9)
При условии, что Q = 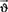 x · Sx =
x · Sx = 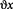 ·πR2mp, средняя скорость потока смеси по эластичному трубопроводу определяется как:
·πR2mp, средняя скорость потока смеси по эластичному трубопроводу определяется как:
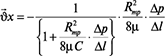 . (10)
. (10)
Полученная зависимость справедлива только при условии
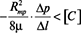 . (11)
. (11)
В противном случае средняя скорость в трубопроводе приобретает отрицательный знак. Это означает, что при больших градиентах давления поток бетонной смеси в эластичном трубопроводе теряет стабильность в связи с возникновением автоколебательного движения смеси [5]. При наличии волнового процесса наблюдается явление возвращающей силы от потока смеси на внутренние стенки трубопровода.
Таблица 1. Скорости продольной волны давления Д1тр=50 мм при транспортировании подвижных бетонных смесей
| Д2тр=50 мм П1=10…11 см | l – длина трубопровода, м | ||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| ΔР1=1,2 МПа, μ1= 180 Па·с | 0,052 | 0,026 | 0,017 | 0,0013 | 0,01 | 0,0087 | 0,0074 | 0,0065 | 0,0058 |
| ΔР1=1,2 МПа, μ2= 250 Па·с | 0,038 | 0,019 | 0,013 | 0,0094 | 0,0075 | 0,0063 | 0,0054 | 0,0047 | 0,0042 |
| ΔР1=1,2 МПа,μ3= 300 Па·с | 0,031 | 0,016 | 0,01 | 0,0078 | 0,0063 | 0,0052 | 0,0045 | 0,0039 | 0,0035 |
| ΔР2=0,9 МПа, μ1= 180 Па·с | 0,039 | 0,02 | 0,013 | 0,0098 | 0,0078 | 0,0065 | 0,0056 | 0,0049 | 0,0043 |
| ΔР2=0,9 МПа, μ2= 250 Па·с | 0,028 | 0,014 | 0,0094 | 0,007 | 0,0056 | 0,0047 | 0,004 | 0,0035 | 0,0031 |
| ΔР2=0,9 МПа, μ3= 300 Па·с | 0,023 | 0,012 | 0,0078 | 0,0059 | 0,0047 | 0,0039 | 0,0034 | 0,0029 | 0,0026 |
| ΔР3=0,7 МПа, μ1= 180 Па·с | 0,03 | 0,015 | 0,01 | 0,0076 | 0,0061 | 0,0051 | 0,0043 | 0,0038 | 0,0034 |
| ΔР3=0,7 МПа, μ2= 250 Па·с | 0,022 | 0,0011 | 0,0073 | 0,0055 | 0,0044 | 0,0037 | 0,0031 | 0,0027 | 0,0024 |
| ΔР3=0,7 МПа, μ3= 300 Па·с | 0,0018 | 0,0091 | 0,0061 | 0,0046 | 0,0037 | 0,003 | 0,0026 | 0,0023 | 0,002 |
Примечание: подвижность смеси П1=10…11 см, вязкость μ1= 180 Па·с; μ2= 250 Па·с; μ3= 300 Па·с
Таким образом, уравнение (11) позволяет проанализировать работу эластичных трубопроводов, по которым транспортируется бетонная смесь при использовании растворобетононасосов и в отдельных случаях бетононасосов. В результате проведенного анализа функционирования таких трубопроводов разных диаметров и длин, работающих при разных давлениях и транспортирующих бетонные смеси различной подвижности, можно дать рекомендации по устойчивой их эксплуатации. Проведены исследования работы различных эластичных трубопроводов с учетом их диаметра и сделаны заключения, при каких условиях их работы не нарушается условие (11), т.е. в трубопроводах происходит стабильное движение бетонной смеси при полном отсутствии автоколебательных явлений в эластичном трубопроводе, которые могут вызвать явления расслаиваемости бетонной смеси.
Таблица 2. Скорости продольной волны давления Д1тр=100 мм при транспортировании подвижных бетонных смесей
| Д2тр=100 мм П1=10…11 см | l – длина трубопровода, м | ||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| ΔР1=1,2 МПа, μ1= 180 Па·с | 0,0083 | 0,0042 | 0,0028 | 0,0021 | 0,0017 | 0,0014 | 0,0012 | 0,001 | 0,0009 |
| ΔР1=1,2 МПа, μ2= 250 Па·с | 0,006 | 0,003 | 0,002 | 0,0015 | 0,0012 | 0,001 | 0,0009 | 0,0008 | 0,0007 |
| ΔР1=1,2 МПа, μ3= 300 Па·с | 0,005 | 0,0025 | 0,0017 | 0,0013 | 0,001 | 0,0008 | 0,0007 | 0,0006 | 0,0006 |
| ΔР2=0,9 МПа, μ1= 180 Па·с | 0,0063 | 0,0031 | 0,0021 | 0,0016 | 0,0013 | 0,001 | 0,0009 | 0,0008 | 0,0007 |
| ΔР2=0,9 МПа, μ2= 250 Па·с | 0,0045 | 0,0023 | 0,0015 | 0,0011 | 0,0009 | 0,0008 | 0,0006 | 0,0006 | 0,0005 |
| ΔР2=0,9 МПа, μ3= 300 Па·с | 0,0038 | 0,0019 | 0,0013 | 0,0009 | 0,0008 | 0,0006 | 0,0005 | 0,0005 | 0,0004 |
| ΔР3=0,7 МПа, μ1= 180 Па·с | 0,0049 | 0,0024 | 0,0016 | 0,0012 | 0,001 | 0,0008 | 0,0007 | 0,0006 | 0,0005 |
| ΔР3=0,7 МПа, μ2= 250 Па·с | 0,0035 | 0,0018 | 0,0012 | 0,0009 | 0,0007 | 0,0006 | 0,0005 | 0,0004 | 0,0004 |
| ΔР3=0,7 МПа, μ3= 300 Па·с | 0,0029 | 0,0015 | 0,001 | 0,0007 | 0,0006 | 0,0005 | 0,0004 | 0,0004 | 0,0003 |
Примечание: подвижность смеси П1=10…11 см, вязкость μ1= 180 Па·с; μ2= 250 Па·с; μ3= 300 Па·с
На рис. 1, 2 и в табл. 1, 2 представлены графические зависимости скорости волны давления [С] от длины трубопровода для его диаметров Д1тр=50 мм и Д2тр=100 мм при различных давлениях и вязкостях транспортируемых смесей.
Исследования проводились для эластичных трубопроводов Д1тр=50 мм и Д2тр=100 мм, используемых для транспортирования бетонных смесей, имеющих подвижность: П1=10…11 см и соответствующих значениях динамической вязкости μ1= 180 Па·с; μ2= 250 Па·с; μ3= 300 Па·с при следующих перепадах давления в трубопроводах: ΔР1=1,2 МПа; ΔР2=0,9 МПа; ΔР3=0,7 МПа.
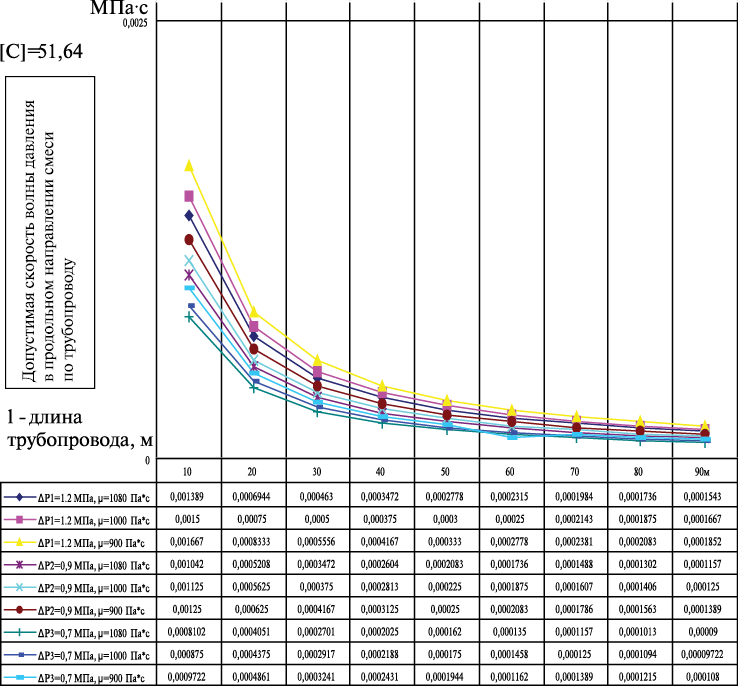
Примечание: подвижность смеси П1=4,5…6 см, вязкость μ1= 1080 Па·с; μ2= 1000 Па·с; μ3=900 Па·с
Для смесей малоподвижных П2=4,5…6 см принимались значения динамической вязкости μ1=900 Па·с; μ2=1000 Па·с; μ3=1080 Па·с при следующих перепадах давления в эластичных (резинотканевых) трубопроводах: ΔР1=1,2 МПа; ΔР2=0,9 МПа; ΔР3=0,7 МПа.
В таблицах 1, 2 приведены расчетные значения скорости волны давления, которые не должны превышать допустимой величины [С] для стабильной работы эластичных трубопроводов при отсутствии продольных автоколебательных явлений.
Исходя из графических зависимостей рис. 1, 2 и расчетных данных таблиц 1, 2 следует, что при транспортировании по эластичным трубопроводам длиной от 10 до 90 м как малоподвижных бетонных смесей (П1=4,5…6 см), так и при транспортировании подвижных бетонных смесей (П2=10…11 см) продольные автоколебательные явления отсутствуют.
Выводы:
1. Предложен новый подход к анализу работы эластичных трубопроводов (шлангов) различной длины для ряда технологических параметров процесса.
2. Продольные автоколебательные явления не наблюдаются в эластичном трубопроводе при диапазоне длин l=10-90 м при транспортировании как малоподвижных, так и подвижных бетонных смесей.
Библиографический список
1. Емельянова И.А., Задорожный А.А., Гузенко С.А., Меленцов Н.А. Двухпоршневые растворобетононасосы для условий строительной площадки. – Харьков: Тимченко А.Н., 2011 – 196 с.
2. Емельянова И.А., Меленцов Н.А., Непорожнев А.С. Многоцелевые двухпоршневые растворобетононасосы для работы в условиях строительной площадки // Междунар. промышл. журнал «Мир техники и технологий» – Харьковская обл., г. Чугуев: ООО Редакция «Мир техники и технологий», 2013, с. 32-34.
3. Волобуев А.Н., Толстоногов А.П. Особенности течения вязкой жидкости в эластичном трубопроводе // Инженерно-физический журнал, 2009. – Т. 82, № 4, с. 751-757.
4. Волобуев А.Н., Толстоногов А.П. Гидродинамика потока в эластичном трубопроводе // Инженерно-физический журнал, 2004. – Т. 77, № 5, с. 88-93.
5. Волобуев А.Н., Толстоногов А.П. Нелинейное уравнение Шредингера в задаче гидроупругости // Инженерно-физический журнал, 1994. – Т. 66, № 2, с. 222-225.