В статье приводятся данные моделирования прочностных свойств тяжелых бетонов при двухосном и трехосном пропорциональном сжатии. Модель разработана по результатам испытаний бетонов в условиях одноосного сжатия. Элементы структуры моделируются случайными величинами, распределенными по нормальному закону. Даны аналитические зависимости и выполнено сравнение результатов моделирования с известными теоретическими и экспериментальными данными.
УДК 624.012.4-183.2
С.В. ЦВЕТКОВ, канд. техн. наук, главный конструктор, ЗАО «Управление специальных и строительных работ», г. Санкт-Петербург
Ключевые слова: прочность, двухосное сжатие, трехосное пропорциональное сжатие, напряжение сжатия, случайная величина, элементы структуры
Keywords: strength, biaxial compression, three-axis proportional compression, compressive stress, random variable, of structural elements
Существующие в настоящее время критерии прочности тяжелого бетона в основном получены из анализа экспериментальных данных и их последующей математической обработки. Данный подход имеет свои плюсы. Вместе с тем разнообразие свойств бетонов, обусловленное особенностями его структуры, в значительной мере препятствует обобщению получаемых результатов.
В настоящей статье сделана попытка на основании экспериментальных данных по одноосным испытаниям бетона получить зависимости для определения его прочности в условиях двух- и трехосного пропорционального сжатия.
Процессы разрушения структуры бетона под нагрузкой подробно представлены в фундаментальной работе О.Я. Берга [2]. Разрушение бетонного образца при сжатии происходит от образования вертикальных трещин отрыва. Нижняя граница напряжений сжатия, при которых появляются первые микротрещины отрыва, называется нижней параметрической точкой и обозначается RТ0. С дальнейшим ростом напряжений сжатия происходит рост микротрещин, их переход в магистральные трещины и последующее разрушение образца при напряжениях Rb.
Можно предположить, что напряжения сжатия являются «характеристикой» прочности элементов структуры бетона, отвечающих за развития трещин отрыва. Зададим распределение прочности элементов структуры бетона по нормальному закону, в котором минимальное значение «характеристики» прочности структуры соответствует RТ0 при их среднем значении прочности Rb.
Среднее значение RT0 для тяжелых бетонов различной прочности по зависимостям [3] составляет (0,33-0,35) Rb. Тогда в диапазоне напряжений от 0 до Rb находятся практически 50% (не менее 49,85%) всех возможных значений прочности элементов структуры, отвечающих за образование трещин отрыва при разрушении бетона в условиях одноосного сжатия. Для нормального распределения имеем: математическое ожидание соответствует среднему значению прочности бетона при одноосном сжатии – М=Rb, а среднеквадратическое отклонение определится как S=0,5 (Rb – RT0).
Рассмотрим модель разрушения бетона в условиях одно- и двухосного сжатия [10]. Для чего из значений, распределенных по нормальному закону с М=Rb и S=0,5 (Rb – RT0), выбирается не менее 100 значений «прочности» σ0i (где i=0, …, 100), которые помещаются в узлы правильной квадратной решетки. Задаются напряжения σ3, при σ3≥σ0i узел считается разрушенным. Критерий разрушения – появление цепочки взаимосвязанных разрушенных узлов, пересекающих исходную решетку в произвольном направлении (схема рис. 1 на примере решетки 5х5). Такое разрушение назовем неориентированным. Появление данной цепочки происходит примерно при 50% разрушенных узлов, что соответствует заданному значению прочности бетона Rb – случай одноосного сжатия (σ3, σ2=σ1=0).

Решетка 5х5, Rb=10,0 МПа, RT0=2,0 МПа.
Разрушено узлов – 12 шт.(48%), σ3max=10,156 МПа.
При двухосном сжатии (σ3≥σ2; σ1=0) разрушение происходит также от образования трещин отрыва, однако наблюдается изменение их положения. Трещины концентрируются в плоскости действия главных сжимающих напряжений σ2 и σ3, то есть имеет место их определенная ориентация. Назовем такое разрушение ориентированным. Блокировка произвольного направления приведет к тому, что разрушение наступит при большем количестве разрушенных узлов (см. пример на схеме рис. 2). Увеличение количества разрушенных узлов с 50% до (65-75)% приведет и к росту значений напряжений σ3. Причем чем выше значения RT0, тем менее значим прирост прочности.
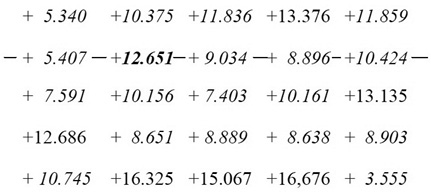
Решетка 5х5, Rb=10,0 МПа, RT0=2,0 МПа.
Разрушено узлов – 19 шт.(76%), σ3max=12.651 МПа.
Если максимальный прирост прочности, происходящий при ориентированном разрушении, составляет от 12-15% до 25-30% в зависимости от значения RT0, то для оценки влияния бокового обжатия при невысоких значениях σ2 целесообразно рассмотреть следующую модель.
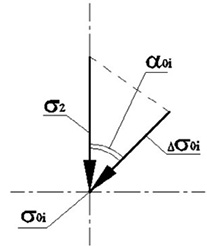
При двухосном сжатии часть элементов структуры, ответственных за развитие трещин отрыва, блокируется боковым давлением и либо делает их разрушение невозможным, либо несколько затрудняет. Смоделируем данную ситуацию следующим образом: для каждого узла исходной решетки задается угол α0i к плоскости действия главных сжимающих напряжений (схема представлена на рис. 3). Значения угла α0i задавались дискретными (00, 300, 600, 900) и распределялись по узлам случайным образом. В зависимости от угла α0i к «прочности» узла σ0i добавлялась величина ∆σ0i=σ2*соsα0i.
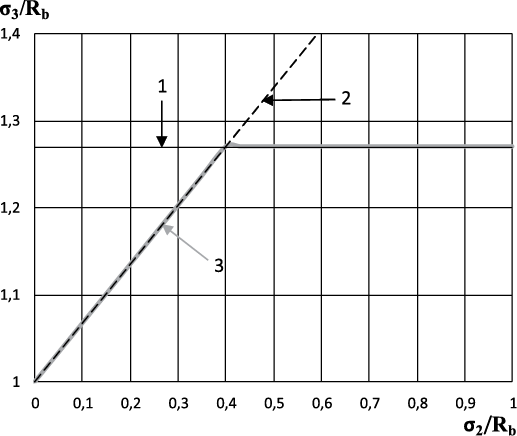
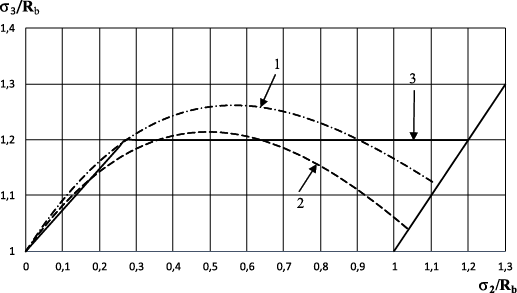
Рассмотрим два независимых случая с последующим совмещением этих двух событий. На рис. 4 график 1 соответствует максимальному увеличению прочности при данном значении RT0, т.е. ориентированному разрушению. График 2 представляет неориентированное разрушение с учетом прироста прочности каждого узла решетки ∆σi. Точка пересечения этих двух прямых (графиков) соответствует случаю, когда прирост прочности при неориентированном разрушении становится равен увеличению прочности при ориентированном разрушении. Таким образом, получается итоговый график 3 в координатах (σ3/Rb – σ2/Rb).
Аналитические зависимости для определения прочности бетона при двухосном сжатии:
– при уровне бокового обжатия σ2/Rb≤(0,6-RT0/Rb) имеет место линейный рост прочности бетона:
σ3= Rb+[0,3(Rb-RT0)*σ2/Rb]/(0,6-RT0/Rb), (1)
– при уровне бокового обжатия σ2/Rb>(0,6-RT0/Rb):
σ3= Rb+0,3(Rb-RT0), (2)
Для Rb=10,0 МПа и RT0=2,0 МПа:
σ3=Rb+0,3(Rb-RT0)=10,0+0,3(10,0-2,0)=12,4 МПа (по результатам моделирования σ3=12,8 МПа);
– для Rb=40,0 МПа и RT0=16,0 МПа: σ3=Rb+0,3(Rb-RT0)=40,0+0,3(40,0-16,0)=47,2 МПа (по результатам моделирования σ3=46,0 МПа).
Графическое сравнение результатов представлено на рис. 5.
При трехосном пропорциональном сжатии прочность бетона определяется зависимостью вида:
σ3=Rb+k σ1 (3),
где Rb – призменная прочность бетона; σ3, σ1=σ2 – главные сжимающие напряжения; k – коэффициент эффективности бокового обжатия. Зависимость (3) представлена в работе [8], в которой коэффициент k (в работе [8] обозначен «m») – условная постоянная величина, определяемая как отношение прочности материала при сжатии к его фиктивной прочности при условном растяжении. Как показали исследования для бетона, k – это переменная величина [6], характеризующая влияние бокового обжатия на повышение прочности при трехосном пропорциональном сжатии σ3>σ1=σ2.
При трехосном пропорциональном сжатии (σ1=σ2 ≤ 0,075σ3), картина разрушения бетона аналогична случаю одноосного сжатия – трещины отрыва с углом наклона 10-150 к продольной оси образца [4]. С дальнейшим ростом бокового обжатия происходит увеличение угла наклона трещин, и при σ1=σ2≥0,2σ3 его значение приближается к 450, а разрушение начинает носить сдвиговой характер.
При σ1=σ2=0 имеет место одноосное сжатие (разрушение при σ3=Rb) и первые трещины отрыва появляются при напряжениях RT0. Наибольшее значение напряжений сжатия для образования трещин отрыва составит σ3=Rb+(Rb-RT0)=(2Rb-RT0), что с учетом сохранения общей картины разрушения образца будет иметь место при напряжениях бокового обжатия σ1=σ2=0,075σ3.
Значение k для уровня обжатия σ1/σ3=0,075 применительно к зависимости (3), определится как:
k=(Rb-RT0)/0,075(2Rb-RT0) (4)
Определим k для граничного значения σ3>σ2=σ1=0,2σ3. Известно, что вне зависимости от уровней бокового обжатия и следующего за этим типом разрушения в бетоне первоначально появляются трещины отрыва [2, 5]. В этом случае соотношение вида (3) можно трактовать следующим образом: первое слагаемое определяет напряжения появления трещин отрыва, второе – увеличение прочности применительно к последующему механизму разрушения. Для механизма отрыва в нашем случае первое слагаемое – это величина (2Rb – RТ0). Для сдвигового механизма разрушения при σ3>σ2=σ1=0,2σ3 рассмотрим модель, приведенную на рис. 6.
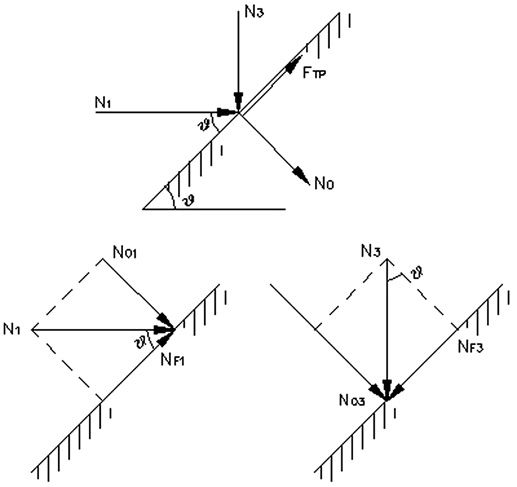
Определим второе слагаемое из условия предельного равновесия:
NF3=NF1+Fтр,
N3 sinϕ=N1 cosϕ + f (N1 sinϕ + N3 cosϕ),
N3=N1(cosϕ+ f sinϕ)/(sinϕ-f cosϕ) (5),
где N01=N1sinϕ; NF1=N1cosϕ; N03=N3cosϕ; NF3=N3sinϕ; Fтр=N0(N01+N03)f, f – коэффициент трения скольжения.
Силы N1 и N3 действуют на горизонтальную (площадь F1) и вертикальную (площадь F3) проекции наклонной площадки (площадь F), F1=Fsinϕ; F3=Fcosϕ.
При значении ϕ=450 sinϕ=cosϕ, тогда F1=F3=F0.
Соответственно, 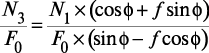 , откуда:
, откуда:
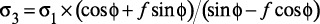 ,
,
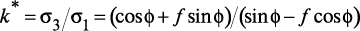 , (6)
, (6)
Для пары «бетон – песок» и «бетон – цемент» коэффициент трения лежит в диапазоне 0,55≥f≥0,45. При значении угла ϕ=450 получим k*=2,62-3,43 (среднее k*=3,0). Для бокового обжатия σ1/σ3=0,2 величина σ3 определится как:
σ3=(2Rb- Rт0)+3,0σ1 (7)
Тогда значения k при σ1/σ3=0,2 для формулы (3) составят: для Rb=10,0 МПа при Rт0=0,2Rb=2,0 МПа – k=3,89; для Rb=40,0 МПа при Rт0=0,4Rb=16,0 МПа – k=3,75.
Используя (6), можно попытаться объяснить уменьшение коэффициента эффективности бокового обжатия при росте напряжений бокового обжатия σ1/σ3→1,0. Допустим, что разрушение при высоком боковом давлении переходит на микроуровень структуры бетона, как это имеет место при рассмотрении процесса ползучести [1]. Тогда обоснованным является предположение, что k→1,0. Действительно, одной из составляющей цементного камня является цементный гель, определяющий прочностные свойства цемента [1]. Разрушение геля происходит по площадкам скольжения, расположенным под углом 450, и с коэффициентом трения по данным площадкам – f=0,012 [1]. По (6) получим величину k*=1,0243, что предполагает и k→1,0.
Таким образом, зависимости (3) и (7) указывают на наличие области неразрушимости тяжелых бетонов при σ1/σ3→1,0, что полностью совпадает с выводами, представленными в работе [5].
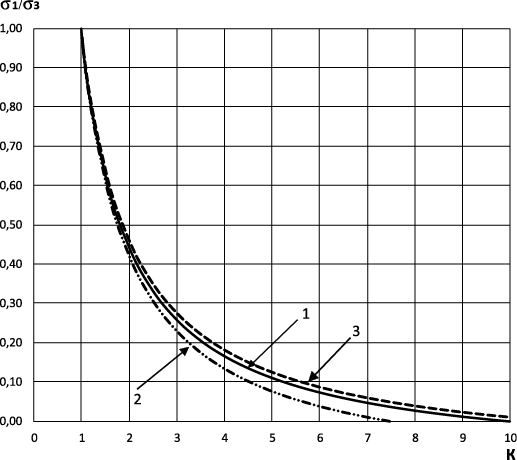
Для построения графиков k=f(σ1/σ3) примем k=1,0 при σ1/σ3=1,0.
Используя данные испытаний бетонов на одноосное сжатие (Rb и RT0), имеем три точки для построения графика в координатах k – σ1/σ3:
– для Rb=10 МПа, RT0=2,0 МПа: при σ1/σ3=0,075 – k=5,93; при σ1/σ3=0,2 – k=3,89; при σ1/σ3=1,0 – k=1,0;
– для Rb=40 МПа, RT0=16,0 МПа: при σ1/σ3=0,075 – k=5,0; при σ1/σ3=0,2 – k=3,75; при σ1/σ3=1,0 – k=1,0.
Задаваясь функцией вида k=1/(a+b*σ1/σ3), получим зависимости (8), (9):
– для Rb=10,0 МПа и RT0=2,0 МПа – k=1/(0,1 + 0,9σ1/σ3) (8);
(при σ1/σ3=0,075 – k=5,97; при σ1/σ3=0,2 – k=3,57; при σ1/σ3=1,0 – k=1,0);
– для Rb=40,0 МПа и RT0=16,0 МПа – k=1/(0,135 + 0,865σ1/σ3) (9).
(при σ1/σ3=0,075 – k=5,0; при σ1/σ3=0,2 – k=3,25; при σ1/σ3=1,0 – k=1,0).
Сравнительный анализ зависимости (3) с использованием (8) (9) с данными других источников представлен в табл. 1 и 2 и на рис. 7.
Таблица 1
| Прочность бетона, Rb, МПа, | Нижняя параметрическая точка, Rt0, МПа | k при σ1/σ3→0,00 | k при σ1/σ3=0,035 | k при σ1/σ3=0,075 | k при σ1/σ3=0,1 | k при σ1/σ3=0,125 | k при σ1/σ3=0,2 | k при σ1/σ3=0,45 |
| 10,0* | 2,0 по [3] | 10,0 по (8) | — | 5,97 по (8) | — | 4,72 по (8) | — | 1,98 по (8) |
| 40,0* | 16,0 по [3] | 8,0 по (9) | — | 5,0 по (9) | 4,52 | 4,12 по (9) | 3,25 | 1,91 по (9) |
| 31,30* | 11,74 по [3] | — | 6,78 | 5,45 | — | 4,40 | — | — |
| 14,0* | 3,51 по [3] | — | 7,14 | — | — | 4,56 | — | — |
| по [6] | — |
mid=10,92; min=9,0 |
mid=8,20; min=7,10 |
mid=6,38; min=5,73 |
mid=5,60 min=5,11 |
mid=4,99; min=4,61 |
mid=3,75; min=3,54 |
mid=2,04; min=2,0 |
| 31,30 [11] | 11,74 по [3] | — | 8,00 | 6,39 | — | 5,26 | — | — |
| 14,00 [11] | 3,51 по [3] | — | 8,00 | — | — | 5,27 | — | — |
| 41,0 [4] | 16,0 по [3] | — | — | — | 3,70 | — | 3,14 | — |
Примечание: *) – по рекомендациям данной статьи
Таблица 2
| Прочность бетона, Rb, МПа, | Нижняя параметрическая точка, Rt0, МПа | σ3 при σ1/σ3=0,035 | σ3 при σ1/σ3=0,15 | σ3 при σ1/σ3=0,075 | σ3 при σ1/σ3=0,1 | σ3 при σ1/σ3=0,125 | σ3 при σ1/σ3=0,2 | σ3 при σ1/σ3=0,45 |
| 10,0* | 2,0 по [3] | — | — | — | — | — | — | 91,75 |
| 40,0* | 16,0 по [3] | — | 93,8 | — | 72,9 | — | 114,30 | 284,70 |
| 31,30* | 11,74 по [3] | 40,9 | — | 53,0 | — | 69,60 | — | — |
| 14,0* | 3,51 по [3] | 18,9 | — | — | — | 32,56 | — | — |
| по [6] | — |
mid=43,42; min=41,51; mid=19,80; min=18,74 |
mid=103,9; min=99,7 |
mid=60,0; min=55,0 |
mid=90,9; min=81,8 |
mid=84,6; min=78,8; mid=37,2; min=28,8 |
mid=160; min=137 |
mid=122,0; min=100,0; mid=487,8; min=400,0 |
| 31,30 [11] | 11,74 по [3] | 43,2 | — | 60,0 | — | 68,90 | — | — |
| 14,00 [11] | 3,51 по [3] | 19,6 | — | — | — | 30,80 | — | — |
| 41,0 [4] | 16,0 по [3] | — | 93,3 | — | 65,0 | — | 112,0 | — |
Примечание: *) – по рекомендациям данной статьи
Испытанный при трехосном сжатии (σ1/σ3>0,2) бетонный образец после разрушения имеет структуру, свойственную, скорее всего, для «спрессованной смеси» составляющих бетона, а не сплошного материала. То же указывается в [8] и для горных пород.
Возможно, состав бетона определяет и угол положения наклонной сдвиговой трещины при трехосном сжатии. Например, смеси щебня с песком, содержащей 50% щебня, соответствует угол внутреннего трения 44,40. Такое содержание крупного заполнителя характерно для обычных бетонов (сдвиговые трещины под углом 450 к вертикальной оси при разрушении в сложном напряженном состоянии). С ростом содержания крупного заполнителя в смеси песка со щебнем происходило увеличение и угла внутреннего трения смеси: при 75% содержании щебня – ϕ=51,90 [7].
Выводы:
Напряжения, соответствующие нижней параметрической точке, зависят не только от класса бетона, но и от технологии его изготовления, условий твердения и многих других факторов. В этой связи при проведении испытания бетона на одноосное сжатие, кроме класса бетона и его прочности Rb, необходима фиксация значений RT0. Целесообразным является экспериментальное исследование углов наклона трещин сдвига к продольной оси образцов различных бетонов в условиях трехосного сжатия.
Библиографический список
1. Ахвердов И.Н. Основы физики бетона. – М.: Стройиздат, 1981. – 456 с.
2. Берг О.Я. Физические основы теории прочности бетона и железобетона. – М.: Госстройиздат, 1962. – 91 с.
3. Берг О.Я., Щербаков Е.Н., Писанко Г.Н. Высокопрочный бетон. – М.: Стройиздат, 1971. – 196 с.
4. Жиренков А.Н., Карцев Н.В., Красновский Р.О. Особенности разрушения существенно неоднородных материалов при одноосном и объемном сжатии // Вестник гражданских инженеров: научно-техн. рецензир. журнал. – СПб: СПбГАСУ, №3, 2009, с. 110-111.
5. Карпенко Н.И. Общие модели механики железобетона. – М.: Стройиздат, 1996. – 394 с.
6. Карпенко Н.И., Карпенко С.Н. К определению прочности бетона при трехосном сжатии // Жилищное строительство, №7, 2013, с. 27-28.
7. Невзоров А.Л. Исследование деформационно-прочностных характеристик смесей щебня с песком // Научный вестник государственного горного университета: научно-техн. журнал. – М.: МИСиС, №3, 2013. с. 60-65.
8. Поль Б. Макроскопические критерии пластического течения и хрупкого разрушения. Ч. 2. Хрупкое разрушение при неодноосных напряженных состояниях // Разрушение. Математические основы теории разрушения: сб. тр. Т. 2. – М: Мир, 1975, с. 408-437.
9. Теличко В.Г., Зиборов Л.А. Исследование прочности при двухосном сжатии бетона класса В-25 // Известия Тульского государственного университета // Технические науки. – Тула: ТулГУ, №1-2, 2009, с. 69-94.
10. Цветков С.В. К оценке статистической модели разрушения бетона при двухосном сжатии // Промышленное и гражданское строительство, №11, 2012, с. 30-31.
11. Рекомендации по определению прочностных и деформативных характеристик бетона при неодноосных напряженных состояниях. – М.: Госстрой СССР, 1986. – 34 с.