Разработана методика исследований колебаний малоразмерных физических моделей зданий с использованием аддитивной технологии. Представлены результаты экспериментального определения резонансных частот при гармонических колебаниях и вычисления сдвига их фаз для двух малоразмерных моделей трехэтажного железобетонного здания с безригельным каркасом. Показано, что применение 3D-принтера позволяет снизить трудоемкость изготовления моделей, а также расширить возможности учета эксплуатационных дефектов зданий и сооружений, полученных от сейсмических, вибрационных и других видов колебательных воздействий на основе физического моделирования.

УДК 699.84

К.Н. МАКАРОВ, доктор техн. наук, профессор, зав. кафедрой строительства; Е.А. ЮРЧЕНКО, канд. техн. наук, доцент кафедры; Е.Е. ЮРЧЕНКО, канд.техн.наук, доцент кафедры; В.Е. ЮРЧЕНКО, студентка, Сочинский государственный университет

Ключевые слова: физические модели, аддитивная технология, резонансные частоты, сейсмические и вибрационные воздействия
Keywords: physical models, additive technology, resonance frequencies, seismic and vibration effects

Знание резонансных частот колебаний зданий и сооружений необходимо для динамического расчета их проч­ности и устойчивости при сейсмических и вибрационных воздействиях [1]. Определение этих частот в натурных условиях – достаточно трудоемкий и дорогостоящий процесс, особенно, если здания имеют сложные формы в плане и по высоте [2-6]. Более приемлемым является метод физического моделирования с использованием малоразмерных моделей.

Однако в строительстве использование моделей ограничено сложностью их изготовления [7, 8], так как материалами являются оргстекло или композиты. В этой связи перспективным представляется применение аддитивных технологий для изготовления моделей строительных конструкций [9, 10].

При физическом моделировании реакции моделей на механические воздействия исследуются с помощью электронных датчиков и компьютерной обработки. Следовательно, материалы моделей должны иметь электроупругие свойства, необходимые для автоматизации сбора и обработки результатов моделирования.

Таким образом, возникают противоречивые требования. С одной стороны, материал модели должен быть из набора, доступного для его применения на 3D-принтере, а с другой – он должен иметь электроупругие свойства.

В работе [11] показано, что указанными свойствами в достаточной степени обладает пластик ABS (акрилонитрилбутадиенстирол – ударопрочная техническая термопластическая смола на основе сополимера акрилонитрила с бутадиеном и стиролом) и, следовательно, из него могут изготавливаться на 3D­-принтерах модели строительных конструкций и целиком зданий и сооружений практически любой сложности.

Для определения частот и форм собственных колебаний деталей или конструкций в технике широко применяется гармоническое возбуждение. Оно имеет наименьшее количество погрешностей при измерениях. В строительстве при натурных испытаниях зданий [3, 5] используется микросейсмический фон естественного и техногенного происхождения, регистрируемый сейсмометрами.

Одной из важнейших характеристик, однозначно определяющей колебания в данный момент времени, как показано в [12], является фаза. Колебания, одновременно протекающие в системе при одной и той же частоте и форме, могут быть сдвинуты относительно друг друга. При совместном рассмотрении таких колебаний для получения достоверных результатов необходимо и достаточно знать не превышающий одного периода сдвиг одинаковых фаз.

В данной работе представлены результаты экспериментального определения резонансных частот при гармонических колебаниях и вычисления сдвига их фаз для малоразмерных (масштаб М 1:100) моделей трехэтажного железобетонного здания с безригельным каркасом. Одна модель из оргстекла (полиметилметакрилат) изготовлена вручную. Другая – из пластика ABS. Она напечатана на 3D-принтере (рис. 1б).

Применяемые для моделирования материалы обладают эффектом электрострикции, который используется в преобразователях, предназначенных для измерения колебаний размеров твердых тел.

Электрострикция – это деформация диэлектрических материалов в электрическом поле, пропорциональная квадрату напряженности электрического поля. Она обусловлена поляризацией, то есть смещением под воздействием внешнего электрического поля молекул, несущих на себе электрические заряды, или изменением ориентации диполей. Эффект электрострикции является квадратичным (четным), поэтому деформация прямо пропорциональна квадрату напряженности поля, причем знак деформации (сжимается или растягивается тело под действием поля) не зависит от направления электрического поля.

Установка для проведения экспериментов состояла из следующих компонентов:

1. Подсистема возбуждения акустических механических колебаний, включающая:

а) источник звука – персональный компьютер Lenovo B 560 или любой другой проигрыватель mp3-файлов;
б) УМЗЧ – усилитель мощности сигнала звуковой частоты (в данном случае магнитола Sony CFS-715S Mega Bass);
в) аккумулятор питания 12 V 7,0 Ah;
г) акустическую систему с динамической головкой 4ГД-35 от электропроигрывателя «Akords-stereo».

2. Соединительные (неэкранированные) и сигнальные (экранированные) силовые провода.

3. Подсистема регистрации вторичных механических колебаний:

а) сигнальные провода с электродами, экранированные, для левого и правого канала;
б) двухканальный микрофонный усилитель с автономным питанием;
в) сигнальные провода для соединения линейного выхода микрофонного усилителя, с линейным входом звуковой карты принимающего компьютера.

4. Принимающий персональный компьютер, работающий как осциллограф.

Во время проведения экспериментов и выполнения измерений электроснабжение в лаборатории отключалось по соображениям минимизации электрических помех. Все агрегаты питались постоянным током от встроенных батарей или аккумуляторов.

Установка монтировалась из отдельных блоков. Акустическая система устанавливалась горизонтально, диффузором акустической системы вверх, а магнитом вниз. Под углы акустической системы ставились виброизоляторы. Между нижним краем акустической системы и опорной поверхностью был оставлен воздушный зазор, равный толщине виброизоляторов. На акустическую систему устанавливалась емкость с сухим крупным песком, имитирующим грунт. Таким образом, вектор акустических механических колебаний был направлен по нормали снизу вверх.

Предварительно для определения частоты механического резонанса системы собиралась подсистема возбуждения акустических механических колебаний.

Источник звука проигрывает файлы с записью синусоидальных колебаний звуковой частоты с шагом дискретизации 1 Герц. Оценка того, какая из частот окажется резонансной, производилась визуально, по резкому увеличению амплитуды механических колебаний модели здания и грунта в емкости. Эксперимент проводился отдельно для каждой из моделей – из пластика ABS и оргстекла. Масса модели из пластика ABS – 104,5 г, масса модели из оргстекла – 98,3 г. Механические характеристики пластиков ABS и оргстекла представлены в табл. 1.

Таблица 1. Механические характеристики моделей

Механические характеристики	Пластик ABS	Оргстекло
Предел прочности при растяжении, МПа	29,6	80-72
Плотность, кг/м3	1020-1080	1190
Модуль Гука, МПа	1270	2800-4900

Осциллограммы записывались для заданных точек, к которым присоединены электроды сигнальных проводов для левого и правого каналов микрофонного усилителя. Провода с электродами были закреплены так, чтобы они не сдвигались относительно исследуемой модели во время проведения эксперимента.

При возбуждении механических колебаний модели она, в силу электроупругих свойств материала, становится источником слабых электромагнитных колебаний. Эти колебания воспринимаются электродами, усиливаются микрофонным усилителем и поступают для регистрации на компьютер, представляющий собой в данном случае низкочастотный двухканальный осциллограф. Методика определения электрических колебаний вокруг электро­упругих материалов позаимст­вована из работы [13].

На основании анализа осциллограмм от испытательных частот 25, 39,40 и 41 Гц вычислены низкие и высокие частоты собственных колебаний моделей. По максимальным значениям сдвига фаз выбирались резонансные частоты моделей. Выбор производился согласно [14]. Метод основан на зависимости между деформацией (сдвигом фаз), измеряемой в градах, и испытательной частотой, измеряемой в Гц. Сдвиг фаз вычислен умножением на 2π разницы во времени между осциллограммой левого и правого канала, деленной на период колебаний низшей из частот.

Поскольку в испытаниях использованы одномерные волны, регистрируемые осциллографом, то волна, распространяющаяся вдоль оси х (ось времени), представляет собой синусоиду. Волна имеет длину λ и частоту f. Тогда при t =0 волна задается выражением D=DM sin(2πx/λ), где D – смещение профиля волны в точке х, DM – амплитуда волны.

Приведенное выражение описывает форму синусоидальной волны, которая движется вдоль оси х со скоростью V. Поскольку V=λf , формулу можно переписать в более удобном виде: D=DM sin [(2πx/λ)-2πt/T], где Т=1/f или в виде D=DMsin(kx—ωt), где ω=2πf =2π/T – круговая частота, k=2π/λ – волновое число. Выражение kx—ωt и соответствующие ему величины являются фазой волны.

Синицыным А.П. [15] предложено учитывать конечную скорость распространения волн и рассматривать действие бегущей волны на основание и сооружение в отдельные интервалы времени по мере ее продвижения. Предложено также волновую картину задавать подвижной нагрузкой, в отличие от стационарного случая при внезапном приложении равнодействующей с эксцентриситетом.

При натурных испытаниях зданий на сейсмическое воздействие, согласно [1], Хачияном Э.Е. учтено его распространение от основания здания с конечной скоростью и произведено интегрирование уравнений движения в конечные интервалы времени. Это дало возможность на каждом этапе существования системы характеризовать ее нарастающим количеством уравнений движения. При этом сама система имеет возрастающее количество степеней свободы, следовательно, различным начальным условиям будут соответствовать различные перемещения этажей, а между инерционными нагрузками на них возникнет сдвиг фаз.

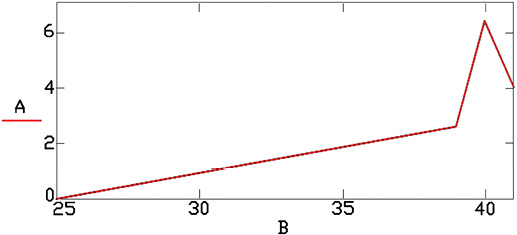
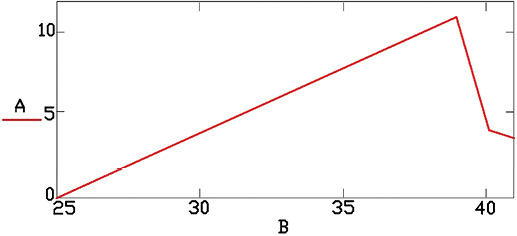
Величины полученных на моделях амплитуд, вычисленных частот и сдвигов фаз представлены в табл. 2, 3 и на рис. 2, 3.

Таблица 2. Результаты испытания модели из оргстекла

Характеристики колебаний	Испытательные частоты, Гц				Резонансная частота
	25	39	40	41
Амплитуды левого канала +/-	+143/-200	+116/-137	+116/-132	+127/-163	40 Гц по характеристике максимального значения сдвига фаз 0,10π
Амплитуды правого канала +/-	+145/-158	+142/-200	+134/-200	+134/-200
Частоты, Гц левого канала низкие/высокие	25/50	10/50	10/50	10/50
Частоты, Гц правого канала низкие/высокие	25/-	9,8/47	10/50	10/45
Сдвиг фаз в долях π	–	0,04	0,10	0,06

Таблица 3. Результаты испытания модели из пластика ABS

Характеристики колебаний	Испытательные частоты, Гц				Резонансная частота
	25	39	40	41
Амплитуды левого канала +/-	+178/-200	+134/-184	+178/-200	+189/-200	39 Гц по характеристике максимального значения сдвига фаз 0,17π
Амплитуды правого канала +/-	+105/-129	+200/-200	+153/-200	+95/-124
Частоты, Гц левого канала низкие/высокие	-/50	10/55	10/50	8,3/43
Частоты, Гц правого канала низкие/высокие	25/-	-/35	10/50	8,3/47
Сдвиг фаз в долях π	—	0,17	0,06	0,05

Выводы:

1. Разработана методика исследований колебаний малоразмерных физических моделей зданий с использованием аддитивных технологий и электрострикционного эффекта.

2. Проведенные эксперименты позволили определить значения:

– резонансных частот для модели из оргстекла – 40 Гц, для модели из пластика ABS – 39 Гц;
– максимального сдвига фаз по записям гармонических колебаний одинаковой частоты по левому и правому каналу, который характеризует резонанс.

3. Изготовление моделей на 3D-принтере из пластика ABS, обладающего электрострикционным эффектом, позволяет снизить трудоемкость изготовления моделей зданий и сооружений и, соответственно, расширить возможности оценки эксплуатационных дефектов зданий и сооружений от сейсмических, вибрационных и других видов колебательных воздействий на основе физического моделирования.

Библиографический список

1. Хачиян Э. Е., Амбарцумян В. А. Динамические модели сооружений в теории сейсмостойкости. – М.: Наука, 1981. – 203 с.

2. ГОСТ 31937-2011. Межгосударственный стандарт. Здания и сооружения. Правила обследования и мониторинга технического состояния. – М.: Стандартинформ, 2014. – 59 с.

3. ГОСТ Р 54859-2011. Здания и сооружения. Определение параметров основного тона собственных колебаний. – М.: Стандартинформ, 2012. – 19 с.

4. Белаш Т.А., Рыбаков П.Л. Здания с подвесными конструкциями в сейсмических районах // Инженерно-строительный журнал, 2016. № 5(65). С. 17–26.

5. Патрикеев А.В., Салатов Е.К. Основы методики динамического мониторинга деформационных характеристик зданий и сооружений // Вестник МГСУ, 2013. № 1. С. 133—138.

6. Татаркин С.А., Малков Р.А., Царапкин С.И., Чекстер К.В. Методика сейсмоакустического исследования прочностных характеристик кирпичной кладки и железобетонных конструкций зданий и сооружений // Развитие городов и геотехническое строительство, 2012. № 14. https://docviewer.yandex.ru/view/431480631.

7. Пересыпкин Е. Н., Юрченко Е. А., Юрченко Е.Е. Экспериментальное исследование модели секции жилого дома типовой серии 1-335 АС при динамических воздействиях // РУП «Институт БелНИИС». Сборник научных трудов. – Минск, 2015, вып. 7. С. 103-111.

8. Бекренев Н.В., Злобина И.В. Экспериментальное исследование форм вынужденных колебаний изделий из композитных материалов при ультразвуковых частотах нагружения // Фундаментальные исследования, 2017. № 12-1. С. 19-24.

9. 3D-печать в строительстве / Ватин Н.И., Чумадова Л.И., Гончаров И.С., Зыкова В.В., Карпеня А.Н., Ким А.А., Финашенков E.A. // Строительство уникальных зданий и сооружений, 2017. № 1 (52). С. 27-46.

10. Камоничкина Н.В., Кочешков И.В. Исследование прочностных характеристик модельного материала, получаемого методом FDM-печати // Аддитивные технологии, 2018. № 3. С. 39-41.

11. Макаров К.Н, Юрченко Е.А, Юрченко Е.Е. Изучение электроупругости консольного образца из пластика ABS, напечатанного на 3D- принтере // Глобализация современных научных исследований. Международный научный симпозиум SWord, 29-30 мая 2018. https://www.sworld.com.ua/index.php/ru/symposia/symposia-ru/simpozium-material/simpoziumarhiv/symposiumru-2018.

12. Исакович М.М., Клейман Л.И., Перчанок Б.Х. Устранение вибраций электрических машин. – Л.: Энергия, 1969. – 216 с.

13.  Бивин Ю.К. Исследование электрических полей при динамическом деформировании полимеров // Журнал технической физики, 2010. т. 80. вып. 6. С. 58-63.

14.  Экспериментальные исследования свойств материалов при сложных термомеханических воздействиях / Под. ред. В.Э. Вильдемана. – М.: Физматлит, 2012. – 204 с.

15. Синицын А.П. Практические методы расчета сооружений на сейс­мические нагрузки. – М.: Стройиздат, 1967. – 144 с.