Композиционный строительный материал является средой с очень специфическими свойствами, где доминирует случайность форм и размеров частиц, физико-механических свойств и условия взаимодействия частиц друг с другом, которые вдобавок зависят от влажности материала [1]. Формирование структуры дисперсных систем во многом обусловливает свойства композиционных материалов, получаемых на их основе. Прочность пространственной структуры дисперсной системы и ее устойчивость, характер поведения при течении, скорость разрушения и восстановления структуры непосредственно связаны друг с другом [2].
УДК 691.539.216
В.В. БЕЛОВ, доктор техн. наук, профессор, советник РААСН, проректор по инновационному развитию, заведующий кафедрой производства строительных изделий и конструкций, П.В. КУЛЯЕВ, ст. преподаватель кафедры конструкций и сооружений, ФГБОУ ВО «Тверской государственный технический университет»
Ключевые слова: дисперсная система, структурообразование, пространственная структура, структурная топология, оптимальная гранулометрия, математическая реконструкция, модель
Keywords: disperse system, structurization, spatial structure, structural topology, optimum granulometriya, mathematical reconstruction, model
Вопросы оптимизации составов дисперсных систем широко рассматриваются многими исследователями в области строительного материаловедения [2, 3, 4 и др.]. Проявление физических явлений уплотнения (заполнения пустот) и раздвижки одних минеральных материалов другими с меньшими размерами зерен и их количественная оценка обеспечивают не только заполнение единицы объема монолитным веществом или материалом, но и формирование оптимальной макроструктуры минеральной части сыпучих смесей [5].
Существуют различные методики достижения оптимальных составов бетона и строительных смесей. Большинство из них базируется на аппроксимации зерновой структуры – представлении ее системой твердых сфер и математическом расчете гранулометрического состава [6, 7 и др.].
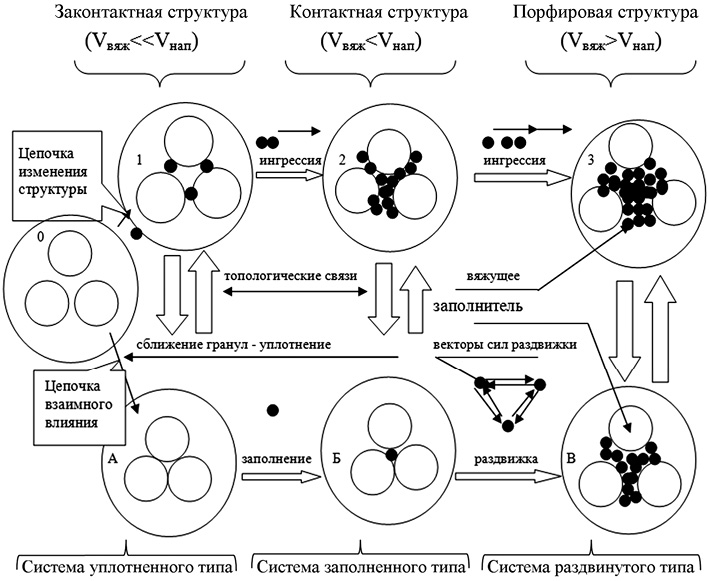
При описании способов проектирования оптимальных упаковок рассматривается сложное комбинирование всех типов схем упаковок в соответствии с физико-химическим взаимодействием компонентов в матрице композита. Данные структуры – контактная, законтактная и порфировая. В структурном представлении комбинация реализуется в зависимости от отношения объема вяжущего Vвяж к объему наполнителя Vнап, и в соподчиненности с тремя схемами эффективной топологии, где ведущая роль принадлежит взаимовлиянию гранул, при котором гранулы большего размера раздвигаются при уплотнении гранулами меньшего диаметра, тем самым создавая поле гранулярно-контактного взаимодействия (рис. 1).
Для подбора состава фракций строятся графики зависимости эффективных коэффициентов от расходов фракций. Графики (рис. 2, 3) увязывают эти коэффициенты для фракции ni/5 мм при проектировании оптимальной упаковки бинарной смеси (строятся по матрице, указанной выше).
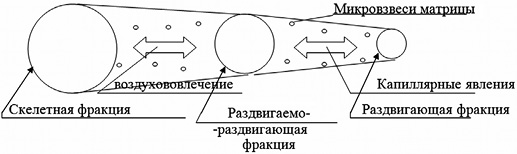
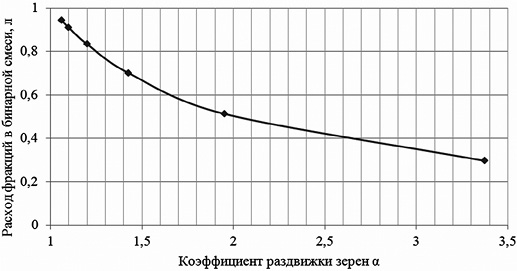
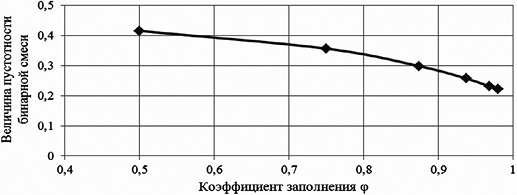
Схема (рис. 4) относится к классификации сыпучей части композита в эффективной топологии, учитывающей взаимодействие и взаимное влияние между частицами. Стрелки между двумя триадами отображают корреляционное соответствие данных топологических структур.
Количественные закономерности представляют собой соотношения количества гранул и контактов между ними (гранул-контактов) для размеров гранул 1 мм, 1 см и 1 дм с приведением их к объемно массовым характеристикам (на 1 кубический метр). Для анализа соотношений приводятся разъяснения символов в используемых зависимостях: G – количество гранул, К – количество контактов между ними ξ=К/G; ν=К×G/ (К+G); µ=(ξ+1)2/ξ; общее количество гранул и контактов вычисляется из выражения N=ν×µ.
В табл. 1 отображено изменение значений G, Vпус, коэффициентов ξ, µ, К/γ, где γ – плотность фракции с соответствующим размером гранул для кубической уплотненной монофракционной упаковки размером в один кубический метр.
Таблица 1. Количественно-контактные коэффициенты
| Диаметр гранулы в единицах | Количество гранул, G | Количество контактов, К | Координационное число, ξ | Координационный коэффициент, µ | Удельное число контактов, ζ=К/γ |
| Метр | 1 | 0 | 0 | ∞ | 0 |
| Дециметр | 103 | 2700 | 2,7 | 5,0704 | 1,227*10-3 |
| Сантиметр | 106 | 1009800 | 1,0098 | 4,000095 | 0,459 |
| Миллиметр | 109 | 1,00099*109 | 1,000998 | 4,000000995 | 454,9991 |
| Микрометр | 1018 | 1,000001*1018 | 1,000000999 | 4 | 4,(54)*1011 |
| Нанометр | 1027 | 1027 | 1 | 4 | 4,(54)*1020 |
Пример расчета количества гранулярных контактов представлен на рис. 5.
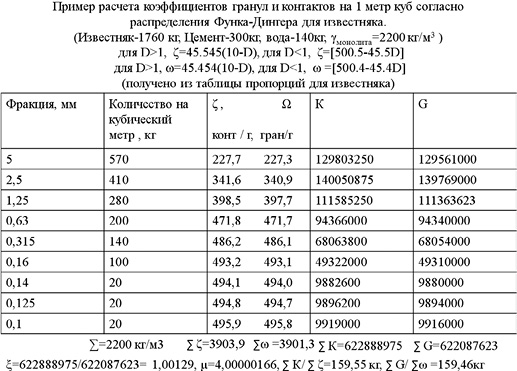
Количественные взаимосвязи справедливы для дисперсных систем со следующими разновидностями макроструктур:
— системы с макроструктурами заполненного типа;
— системы с макроструктурами раздвинутого типа;
— системы с макроструктурами заполненно-раздвинутого типа.
Каждый тип систем обладает индивидуально выраженной количественной взаимосвязью между составом, макроструктурой и показателями физико-механических свойств [8]. Крупнозернистые фракции с большими размерами твердых тел, имеющие точечный контакт между собой, называются скелетными или скелетообразующими фракциями. Смеси, в которых объемы межзерновых пустот заполнены твердыми телами меньших размеров, относятся к категории конгломератных систем заполненного типа.
В системах заполненного типа величина объема межзерновых пустот определяется величиной пустотности скелетной фракции за вычетом объема монолитного твердого тела заполняющей фракции. Один кубометр скелетной фракции имеет величину пустотности, равную Vп1, заполняющая фракция имеет величину пустотности Vп2. Объем монолитного материала заполняющей фракции в 1 м3 насыпного объема составляет Vм2=1–Vп2, м3, а в Vн, м3, расходуемом на заполнение объема межзерновых пустот скелетной фракции,
Vм2 = Vн(1- Vп2), м3.
Таким образом, величина пустотности системы заполненного типа определяется по формуле:
Vпсм = Vп1-Vн(1-Vп2), м3.
Для заполнения объема пустот системы заполненного типа жидким компонентом требуется Vпсм, м3.
Расход скелетной фракции составляет 1 м3, расход фракции с меньшими размерами твердых тел равен Vн2, м3, объем пустот смеси равен Vпсм, м3.
Масса смеси в 1 м3 равна насыпной плотности смеси:
γсм= 1 м3 × γ1+Vн2 × γ2= Gсм, кг/м3.
Объем смеси определяется выражением:
Vсм = Vмон1+Vмон2+Vпсм = 1 м3.
Баланс монолитных объемов, объема пустот или объема жидкого компонента используется для правильности расчетов и дозировки материалов в процессе приготовления смеси. Твердые тела заполняющей фракции, соизмеримые с размерами пустот скелетной фракции, могут заполнять пустоты скелетной фракции только в процессе перемешивания смеси или в процессе послойного заполнения пустот.
Твердые тела заполняющей фракции (в 6,4-6,6 раза меньшие по размерам твердых тел скелетной фракции) обладают способностью заполнять пустоты скелетной фракции подобно жидкости. В процессе перемешивания минеральных материалов в присутствии жидкой фазы обязательно происходит вклинивание мелких твердых тел между телами больших размеров, а между всеми твердыми телами формируются прослойки жидкого компонента.
В процессе перемешивания дисперсных систем заполненного и раздвинутого типов формируются системы заполнено-раздвинутого типа. В системах заполненного типа заполняющая фракция перераспределяется в процессе перемешивания, часть объема этой фракции расходуется на раздвижку, а остальная часть в процессе уплотнения смеси используется для заполнения пустот фракции с большими размерами зерен. При этом пустотность уплотненной системы всегда меньше ее расчетной величины.
Составы систем заполненно-раздвинутого типа рассчитываются с использованием следующих аналитических выражений.
Расход фракции с размерами тел d1:
Vd1=1м3/ α1,, м3.
Расход фракции с размерами тел d2:
Vd2 =Vd1 × (Vпd1+α1-1)/α2.
По другим зависимостям:
Vd2 = φ×Vпd1, при d2/d1 → 1;
Vd2 = Vпd1, при d2/d1 → 0,
где φ – степень заполнения пустот одной фракции зернами другой, его величина определяется эмпирически и колеблется в пределах от 0 до 1. Ее эквивалентом при количественном рассмотрении гранул и контактов является величина полной пустотности в процентах в зависимости от модальности и типа упаковки.
Расход жидкой фазы:
Vж = Vd2 × (Vпd2+α2-1)/1 , м3,
где α1 и α2(α= (1+d2/d1)3) – коэффициенты раздвижки при d1 >> d2.
Если раздвигающий компонент – жидкая фаза, то заполненно-раздвинутая упаковка будет характеризоваться наличием жидких прослоек между всеми зернами системы (рис. 6).
Использование дисперсных систем для изготовления строительных композитов включает несколько последовательных стадий: лабораторные испытания исходных сырьевых материалов, проектирование или подбор смесей с требуемым комплексом показателей физико-механических свойств, промышленное производство дисперсных смесей, получение композиции на их основе с последующим изготовлением строительных изделий и конструкций. При этом решаются вопросы, связанные с установлением качественных и количественных взаимосвязей между составом, структурой (макроструктурой) и свойствами.
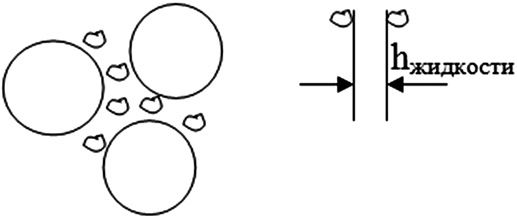
С использованием дисперсных материалов с различными гранулометрическими характерами представляется возможным получение смесей с широкими пределами колебаний объемно-массовых характеристик. Получение материалов с экстремально выраженными свойствами достигается через оптимизирование гранулометрического состава смеси, а также через оптимизирование объемных соотношений между сыпучей смесью и жидкой фазой в процессе приготовления композиций (растворов, смесей для формования, виброуплотнения). Наряду с оптимизированием составов смесей по грансоставу большое значение имеет отношение размеров твердых тел. Система, оптимизированная по грансоставу, является оптимальной и по макроструктуре. Такая система является составной частью оптимизированной композиции, содержащей в своем составе оптимальное количество матрицы (вода – в бетонных смесях, битум – в асфальтобетонных смесях, связующее вещество – в композиционных материалах). Данные характеристики сейчас особенно актуальны, когда развиваются такие системы, как самоуплотняющиеся бетоны (СУБ), портланд-известняковые цементы (группы CEM II/LL), которые нашли отражение в нормах зарубежных стран. Наряду с проблемами оптимизирования дисперсных смесей и композиций в процессе проектирования изделий из мелкозернистых бетонов высокого качества необходимо оптимизирование параметров на всех операциях технологического процесса. Сюда относятся: дозирование фракций, давление, время, температура, направление и величина виброколебаний, параметры внешней среды и др. При проектировании строительных композитов заданной структуры устанавливаются количественные взаимосвязи между объемно-массовыми и гранулометрическими характеристиками дисперсных систем, явлениями уплотнения (заполнения) и раздвижки зерен зернами, объемно-массовыми характеристиками дисперсных смесей и физико-химическими свойствами компонентов бетонов.
Выводы:
Таким образом, решая задачи подбора состава композита, для различных критериев оптимальности, будь то экономия сырьевых материалов или повышение технико-эксплуатационных показателей материалов, необходимо направленно варьировать рецептурные параметры, подбирая требуемые соотношения компонентов, и согласовывать их с выходными свойствами материала. В данном исследовании методом математического моделирования установлены функциональные взаимосвязи между объемно-массовыми параметрами дисперсных материалов, применяемых в производстве строительных композитов. Полученные данные не противоречат существующим независимым исследованиям.
Библиографический список
1. Баранцева Е.А. Процессы смешивания сыпучих материалов: моделирование, оптимизация, расчет / Е.А. Баранцева, В.Е. Мизонов, Ю.В. Хохлова. – ГОУ ВПО «Ивановский государственный энергетический университет им. В.И. Ленина», – Иваново, 2008. – 116 с.
2. Баженов Ю.М. Модифицированные высококачественные бетоны / Ю.М. Баженов, В.С. Демьянова, В.И. Калашников // Научное издание. – М.: Издательство Ассоциации строительных вузов, 2006. – 368 с.
3. Белов В.В. Формирование оптимальной макроструктуры строительной смеси / В.В. Белов, М.А. Смирнов // Строительные материалы, 2009, №9, с. 88-90.
4. Белов В.В. Теоретические основы методики оптимизации гранулометрического состава композиций для изготовления безобжиговых строительных конгломератов / В.В. Белов, М.А. Смирнов // Российская академия архитектуры и строительных наук. Вестник отделения строительных наук. Научное издание. Вып. 15. – Москва – Орел – Курск, 2011, с. 175-179.
5. Белов В.В. Новые принципы определения состава высококачественного бетона / В.В. Белов, М.А. Смирнов // Вестник Тверского государственного технического университета. Вып. 13 / Тверской гос. техн. ун-т. – Тверь, 2008, с. 341-346.
6. Королев Л.В. Анализ упаковки полидисперсных частиц в композитных строительных материалах / Л.В. Королев, А.П. Лупанов, Ю.М. Придатко // Современные проблемы науки и образования, 2007, №6, с. 105-108.
7. Слоэн Н.Дж.А. Упаковка шаров / Н.Дж.А. Слоэн // В мире науки. Scientific American. Издание на русском языке. 1984, №3, с. 72-82.
8. Миронов В.А. Методы оптимизации составов сыпучих систем / В.А. Миронов, А.И. Голубев, – Тверь: ТГТУ, 2003, с. 76.