В работе доказывается необходимость учета при прогнозировании долговечности деревянных соединений их податливости. Показано, что существующая методика прогнозирования долговечности материалов, базирующаяся на положениях термофлуктуационной теории разрушения и деформирования твердых тел, не позволяет с достаточной надежностью прогнозировать долговечность деревянных соединений. Предлагается разработку методики вести в рамках термофлуктуационной концепции путем изучения процессов разрушения и деформирования трех видов деревянных конструкций: элемент сплошного сечения, элемент составного сечения без связей, элемент составного сечения на податливых связях – с последующим сравнением их долговечности (термофлуктуационных констант).
УДК 691.112
С.П. СКВОРЦОВ, магистрант, А.В. ЕРОФЕЕВ, канд. техн. наук, доцент кафедры «Конструкции зданий и сооружений» ФГБОУ ВО «Тамбовский государственный технический университет»
Ключевые слова: деревянные соединения, надежность прогноза работоспособности, податливые связи, флуктуационная концепция
Keywords: wooden connections, reliability of the working capacity forecast, compliant connections, fluctuation concept
Проявление для строительных материалов универсальной температурно-временной зависимости предела текучести, прочности и деформативности делает целесообразным прогнозирование параметров их работоспособности, в т.ч. долговечности, с позиции термофлуктуационной концепции разрушения и деформирования твердых тел.
Данная концепция, в отличие от представлений классической механики пластических деформаций, которая учитывает лишь конкуренцию между силами межатомных связей и внешней приложенной силой, рассматривает тепловое движение атомов как решающий фактор процессов механического разрушения и деформирования. Иначе говоря, в термофлуктуационной концепции, обязанной своему развитию фундаментальным работам школы С.Н. Журкова, разрушение твердого тела перестало считаться критическим событием, наступающим при достижении действующих в материале напряжений критических величин. В термофлуктуационной концепции разрушение тела рассматривается как термоактивационный процесс, который развивается во времени в случае приложения к телу нагрузки, которая уменьшает энергию связей, что, в свою очередь, приводит к изменению расстояния между атомами. Следовательно, с увеличением механического поля происходит ускорение процесса разрыва межатомных или межмолекулярных связей. Направленность приложенной нагрузки делает этот процесс необратимым вследствие накопления элементарных разрывов. Механическое разрушение реализуется через элементарные акты разрыва межмолекулярных или межатомных связей, т.е. разрушение является механотермическим процессом, протекающем во времени, причем время только увеличивает количество тепловых флуктуаций, которые необходимы для реализации механотермического процесса, и само по себе роли не играет.
При экспериментальном изучении температурно-временной зависимости прочности С.Н. Журковым была выведена формула для определения долговечности материала. Развитие научных основ термофлуктуационной концепции позволило объяснить механизм разрушения и вскрыть физический смысл констант, входящих в полученную формулу. Позже С.Б. Ратнером и В.П. Ярцевым формула была модифицирована путем введения ограничения предельной температуры, при которой материал может работать, при этом физический смысл констант и трактовка теплового движения атомов как решающего фактора разрушения остались неизменными. Формула получила название обобщенного уравнения Журкова [1] и в настоящее время имеет следующий вид:
 , (1)
, (1)
где τ – долговечность материала или время до наступления одного из предельных состояний, с; R – универсальная газовая постоянная, кДж/моль·К; σ – напряжение, МПа; T – температура, К; τm, U0, γ, Tm – физические константы материала, имеющие для классического случая следующий физический смысл:
τm – минимальное время разрушения твердого тела, характеризующееся периодом колебания той или иной кинетической единицы (атом, группа атомов или сегментов), с;
U0 – максимальная энергия активации процесса разрушения, определяющаяся энергией связей, препятствующей потери целостности тела, причем в металлах она близка к энергии сублимации, в полимерах – к энергии активации процесса термодеструкции, т.е. максимальная энергия активации процесса разрушения численно близка к величине энергии активации распада межатомных связей в твердых телах, кДж/моль;
γ – структурно-механическая константа, характеризующая эффективность механического поля при приложении к телу нагрузки, кДж/(моль·МПа);
Tm – предельная температура существования твердого тела, при которой оно распадается за одно тепловое колебание, К.
Бывают случаи, когда обобщенное уравнение Журкова в классическом виде (1) не может быть применено для определения долговечности строительных материалов. Это происходит тогда, когда прямые температур не сходятся в пучок [2], а образуют семейство параллельных прямых (рис. 1в) или сходятся в пучок при предельно низкой температуре – «обратный пучок» (рис. 1б), а не при предельно высокой – классический случай «прямого пучка» (рис. 1а).
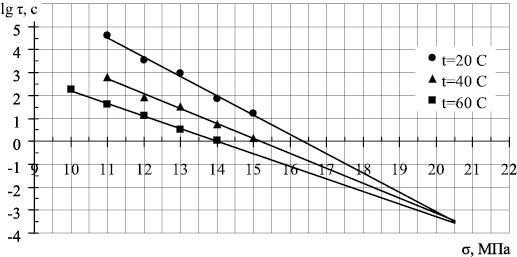
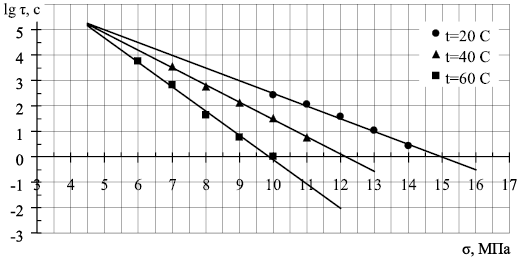
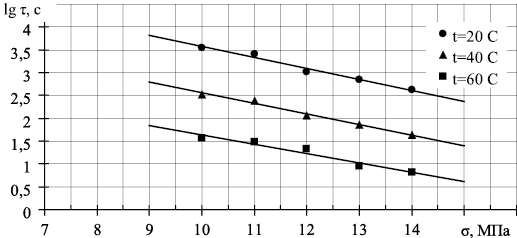
Рис. 1. Зависимость долговечности от напряжения: а – прямой пучок; б – обратный пучок; в – параллельные прямые
Объективная оценка долговечности позволяет рассчитать затраты на проведение текущих и капитального ремонтов здания и, как следствие, численные значения ежегодных амортизационных отчислений. При достижении показателей, количественно отражающих остаточный ресурс эксплуатационных характеристик, принимаются меры по их восстановлению (в ходе текущего и капитального ремонтов), а в случае значительного износа – по сносу или реконструкции здания. Однако анализ формулы (1) показывает, что обобщенное уравнение Журкова позволяет при прогнозировании долговечности материала учитывать только температуру, при которой эксплуатируется материал, и напряжение, действующее на него. Условия эксплуатации, при которых твердое тело работает только в температурно-механическом поле, условно можно считать идеальными. Однако на практике материал эксплуатируется в условиях, отличных от идеальных. Это атмосферные воздействия, работа материала в конструкции и т.д. Отказ от учета реальной работы материала приводит к занижению, а чаще всего к завышению теоретически определенных сроков его службы.
Таким образом, необходимость учета реальной работы твердого тела при прогнозировании срока его службы не вызывает сомнения. Попытки учета влияния атмосферных факторов на долговечность материала в рамках термофлуктуационной концепции делались неоднократно. Поэтому целью настоящей работы является формулировка научной гипотезы учета податливости деревянных соединений при определении их сроков службы, а также определение методов и подходов, позволяющих подтвердить или опровергнуть выдвинутую гипотезу.
Ограниченность размеров лесоматериалов (длина и сечение) обусловливает при изготовлении деревянных конструкций необходимость их соединения между собой, которое может быть выполнено по длине (сращивание), по ширине (сплачивание) или под углом с прикреплением к опорам (анкеровка). Таким образом, в подавляющем большинстве случаев, за исключением деревянных стоек и балок невысокой несущей способности, в чистом виде работу древесины как конструкционного материала рассматривать нельзя. Иначе говоря, необходимо рассматривать работу древесины в соединении, причем следует понимать, что механизм разрушения и деформирования в зависимости от вида и характера работы соединения меняется, что приводит к изменению долговечности. Соединения деревянных конструкций по характеру работы делятся на 5 основных групп, которые, в свою очередь, по виду связи подразделяются на 4 группы:
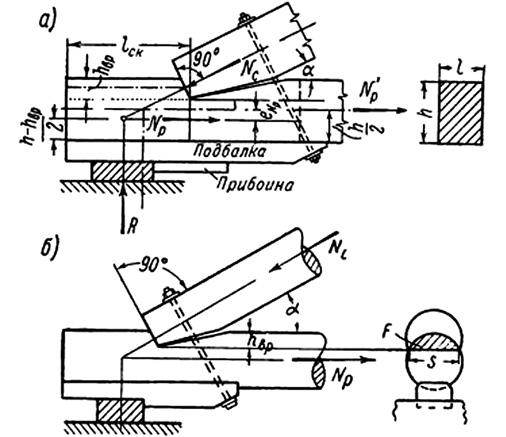
1. Соединения без специальных связей, требующих расчета (упоры и врубки). Это конструктивные врубки (соединения, в которых возникают усилия намного меньше их несущей способности – соединения в четверть, в шпунт, в полдерева и косой прируб). Лобовые упоры (рис. 2): поперечные – соединение двух стержней под прямым углом, когда торец сжатого стержня упирается в пласт другого и закрепляется конструктивными накладками на болтах; продольные – соединение обрезанного под прямым углом конца сжатого стержня с опорой, диафрагмой узла или торца другого такого же стержня в сжатом стыке; наклонные – соединение двух сжатых стержней под углом меньше прямого и лобовые врубки – соединение двух стержней под углом, например, соединение малопролетных ферм и подкосных систем. Соединения без специальных связей применяются, как правило, при построечном изготовлении конструкции.
2. Соединения с деревянными связями, работающими на сжатие или изгиб. К таковым относятся соединения на шпонках (рис. 3). Шпонки, работающие на сжатие, представляют собой призматические бруски древесины, плотно вставляемые в вырезанные в кромках соединяемых элементов гнезда; колодках. Под ними понимаются шпонки, у которых толщина больше, чем высота гнезда; нагелях (работа на изгиб). В связи с тем, что соединения с деревянными связями требуют значительных затрат ручного труда, их считают устаревшим типом соединения и применяют редко, как правило, при построечном изготовлении деревянных конструкций.
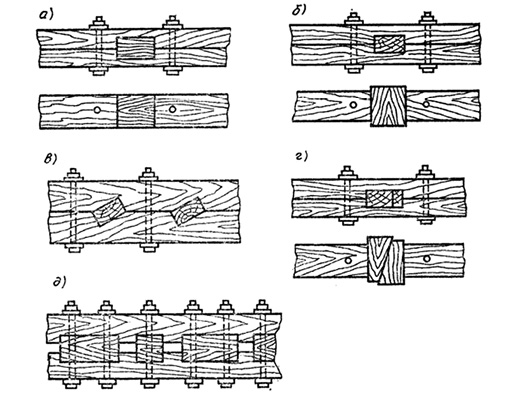
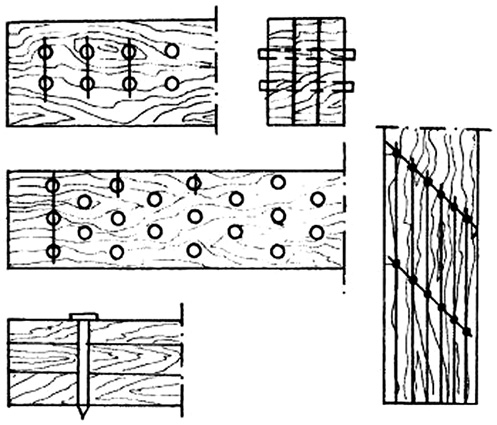
3. Соединения с металлическими связями, работающими на сжатие, растяжение или изгиб. Металлические соединения являются универсальными и широко используются как при построечном, так и при индустриальном способе изготовления деревянных конструкций. К основным металлическим связям относятся гвозди, болты, винты, когтевые шайбы (рис. 4) и хомуты.

4. Соединения с клеевыми связями (рис. 5). В данном случае связи, как правило, работают на сдвиг. Клеевые соединения, хотя и относятся к наиболее технологичным и применяемым при заводском изготовлении деревянных конструкций, в отличие от первых четырех видов, являются неподатливыми, поэтому в контексте данной работы рассматриваться не будут.
На основании анализа приведенной классификации деревянных соединений по критериям универсальности и перспективности использования в строительстве в качестве объекта исследования выбраны податливые деревянные соединения на металлических связях (гвоздях) (рис. 6). Предметом исследования являются процессы разрушения и деформирования деревянных соединений на металлических связях.
Чтобы понять характер работы элементов на податливых связях, достаточно рассмотреть 3 вида балок [3, 4], работающих на поперечный изгиб, у которых нагрузки, пролеты и поперечные сечения одинаковые (рис. 7). Первая балка имеет цельное сечение (Ц), вторая – из двух брусьев без всяких связей (О) и третья – из двух брусьев с податливыми связями (П). При изгибе деформации составной балки на податливых связях будет больше деформаций балки цельного сечения, но меньше деформаций балки без связей:
fЦ<fП <fО (2)
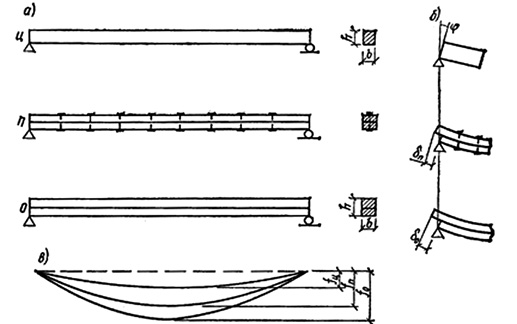
Следовательно, составная балка на податливых связях занимает промежуточное положение между балкой цельного сечения и составной балкой без связей, поэтому можно утверждать, что при деформировании под нагрузкой в составной балке на податливых связях, в отличие от балки цельного сечения, произойдет, кроме поворота опорного сечения, сдвиг δП верхнего пояса относительно нижнего.
Геометрические характеристики этих балок будут подчиняться следующим зависимостям:
IЦ >IП>IO (3)
WЦ>WП>WO (4)
Данные неравенства вытекают из условия того, что:
IЦ=bh3/12, а IО=(b(h/2)3/12+(b(h/2)3/12+bh3/48
Из неравенств (3) и (4) следует, что геометрические характеристики составной балки на податливых связях (IЦ, WЦ) можно выразить через геометрические характеристики балки цельного сечения умножением на коэффициенты kw и kж, получившие название коэффициентов податливости. Они всегда меньше 1 и учитывают податливость связей. Тогда:
WП=kW WЦ , kW<1 (5)
IП=kж IЦ, kж<1 (6)
Прогиб балки на податливых связях увеличивается соответственно уменьшению момента инерции.
Рассмотренная методика учета податливости путем ввода в расчетные формулы коэффициентов податливости при расчете составных стержней на прочность и деформации впервые была разработана в нашей стране и является общеизвестной. На основании положений данной методики и с учетом физического смысла констант обобщенного уравнения Журкова можно предположить, что для учета податливости деревянных соединений при определении их долговечности необходимо и достаточно введение в уравнение (1) коэффициента податливости, изменяющего структурно-механическую константу γ. Введение аналогичных коэффициентов для других констант противоречит основным положениям термофлуктуационной концепции разрушения и деформирования твердого тела, а именно их физическому смыслу для классического случая. Период колебания кинетическое единицы материала, температура его существования и максимальная энергия активации процесса разрушения зависят, грубо говоря, только от вида материала, но не от напряженно-деформированного состояния, вида поперечного сечения, места и характера приложения нагрузки. В данном случае за всю механическую составляющую отвечает только структурно-механическая константа.
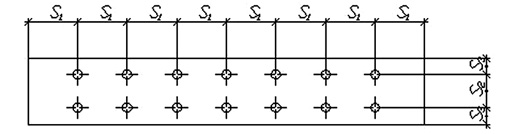
Таким образом, для подтверждения выдвинутой гипотезы необходимо определить термофлуктуационные константы обобщенного уравнения Журкова для трех видов балки. Первый вид балки имеет цельное сечение (Ц), второй состоит из двух брусьев без всяких связей (О), третий – из двух брусьев с податливыми связями (П). Испытание предполагается вести на образцах длиной 120 мм (расчетный пролет однопролетной шарнирно опертой балки составляет 100 мм при центральном приложении нагрузки через рычаг с определенным передаточным отношением), сечением b×h=20×20 мм с расстановкой связей согласно рис. 8.
Выводы:
Экспериментальное доказательство сформулированной в работе научной гипотезы, на что и будет направлена дальнейшая работа, позволит приблизить идеализированные теоретические представления о работоспособности соединений к реальным условиям эксплуатации и разработать в рамках термофлуктуационной концепции разрушения и деформирования твердого тела методику надежного прогнозирования срока службы конструкций на податливых связях.
Библиографический список
1. Ратнер С.Б., Ярцев В.П. Физическая механика пластмасс. Как прогнозируют работоспособность? – Москва: Химия, 1992, с. 320.
2. Ярцев В.П., Кисилева О.А. Прогнозирование поведения строительных материалов при неблагоприятных условиях эксплуатации. Издательство ТГТУ, 2009, с. 124.
3. Асамидинов Ф.М. Исследование способов определения реакции связей в статически определимых балках // Территория науки, №1, 2015, с. 97-102.
4. Зулпуев А.М., Насиров М.Т., Абдыкеева Ш.С. Влияние нормальных усилий на работу статически неопределимых систем // Территория науки, №3, 2015, с. 45-56.