В статье показана математическая модель, выражающая зависимость прочности бетона от расходов цемента 250-550 кг и воды 130-230 л на 1 м³ бетона при заданной активности (марке) цемента по ГОСТ 30744-2001.

УДК 691.328 ББК 38.626.1

А.И. ШУМКОВ, канд. техн. наук

Ключевые слова: математическая модель, бетон, прочность, цемент, заполнитель, вода, цементный камень
Keywords: mathematical model, concrete, strength, cement, aggregate, water, cement stone

В [1] было показано, что прочность бетона понижается по мере увеличения количества воды в бетонной смеси, а кривые зависимости прочности бетона при сжатии Rб, МПа, от расхода воды имеют максимум, если расход цемента Ц, кг/куб. м бетона – величина постоянная. Эта закономерность была обнаружена профессором И.Г. Малюгой в 1895 году, кривая которого показана в [2], а также на сайте http://msd.com.ua/str/46.html

При недостатке воды бетонная смесь получается слишком жесткой и неудобоукладываемой. Снижение прочности бетона в этой части кривых объясняется наличием многочисленных воздушных пустот, образующихся от недоуплотнения смеси из-за слишком высокой вязкости цементного теста и недостаточного его объема для обмазки зерен заполнителей и заполнения их межзерновых пустот. По мере увеличения расхода воды (при постоянном Ц) объем цементного теста возрастает, а его вязкость понижается так, что становится возможным не только обмазать зерна заполнителей и заполнить тестом их межзерновые пустоты, но и создать некоторый оптимальный избыток теста, что обеспечивает наиболее плотную укладку бетонной смеси с наименьшими дефектами. Максимум на кривых прочности соответствует оптимальному для данного способа уплотнения расходу воды, при котором смесь укладывается наиболее плотно. При большем расходе воды бетонная смесь укладывается также плотно, но прочность бетона уменьшается (правая ветвь кривой Малюги и кривых, показанных в [1]) вследствие того, что лишь часть воды (по [2] – 15-20% от массы цемента) вступает в химическую связь, а избыточная вода образует капиллярные поры, и их количество в затвердевшем цементном камне и бетоне тем больше, чем выше расход воды. Поэтому плотность и прочность бетона понижаются.

Те же явления происходят и в том случае, если принять за постоянную величину расход воды, изменяя расход цемента. Только в первом случае основное влияние на прочность бетона оказывает расход воды, а во втором – расход цемента.

В обоих случаях имеет место изменение водоцементного отношения В/Ц, которое учитывает совместное влияние на прочность бетона и расхода цемента, и расхода воды. Поэтому величина В/Ц стала важнейшей характеристикой прочности бетона и других его свойств.

Как отмечено в [3], зависимость прочности бетона от В/Ц вытекает из физической сущности формирования структуры бетона. Минимальное В/Ц, необходимое для реакций гидратации цемента, находится в интервале 0,15-0,25 в зависимости от качества цемента и срока твердения. Для придания же бетонной смеси пластичности в бетон вводят воды значительно больше. На практике чаще всего принимают В/Ц=0,4-0,7, но оно может быть и меньше 0,4, и больше 0,7. Однако при очень низких В/Ц, даже при значительно повышенных расходах цемента и воды, не удается получать удобообрабатываемые бетонные смеси и необходимую слитную структуру бетона без пустот. Вследствие чего с уменьшением В/Ц ниже оптимального прочность бетона также начинает уменьшаться, как и при постоянном расходе воды с избыточно повышенным расходом цемента. Так, при В/Ц=0,2 бетонная смесь является почти сухой, и ее нельзя качественно перемешать и уложить. Определенную роль в снижении прочности бетона в этом случае играет и тот факт, что для гидратации цемента необходим некоторый избыток воды по сравнению с тем количеством, которое непосредственно вступает в химическую связь с цементом. Резкое уменьшение этого избытка воды приводит к замедлению гидратации цемента и, следовательно, к понижению прочности бетона.

При повышении В/Ц сверх оптимального значения избыточная вода, не вступившая в химические реакции с цементом, остается в бетоне, как отмечалось выше, в виде водяных пор и капилляров или испаряется, оставляя воздушные поры, и их тем больше, чем выше В/Ц. В результате плотность и прочность цементного камня и бетона понижаются по мере дальнейшего увеличения В/Ц, как и при постоянном Ц при увеличении В.

Однако в действующей практике мы не наблюдаем максимума прочности бетона на зависимостях Rб от В/Ц. Обычно мы видим увеличение прочности бетона с понижением В/Ц и именно так трактуем закон В/Ц.

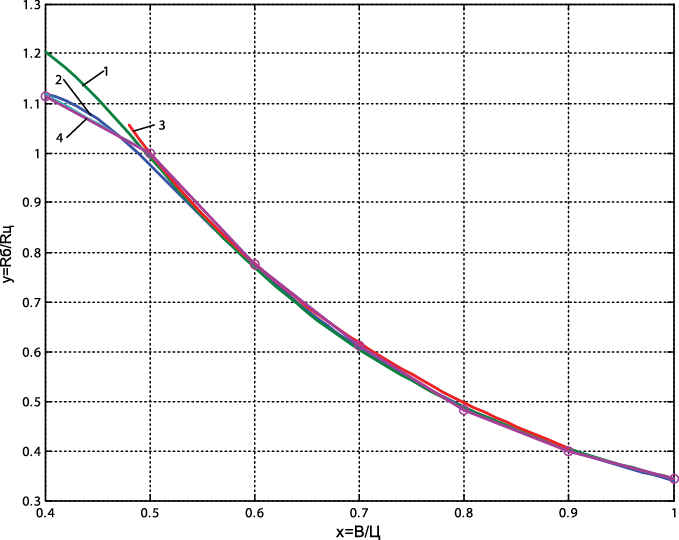
По приведенной в [4] номограмме, обобщающей практический опыт Германии за многие годы, зависимость прочности бетона от В/Ц для конкретных евромарок цемента выражена серией кривых, не имеющих максимума прочности в интервале В/Ц=0,3-0,4. На основе этой номограммы в [1] показаны математические модели зависимости отношения прочности бетона к марке цемента Rб/Rц=y от В/Ц=x.

При варьировании В/Ц от 0,3 до 0,6 с аппроксимацией уравнением параболы y=a*x2+b*x+c получены коэффициенты: a=-4,37; b=2,61; c=0,78, показавшие максимум y=Rб/Rц при В/Ц=0,3, а при варьировании В/Ц от 0,3 до 1,0 с аппроксимацией уравнением:

y=1/(a*x+b/x+c) (1)

получены коэффициенты a=5,14; b=0,67; c=-2,9, показавшие максимум y=Rб/Rц при В/Ц=0,36, которого в экспериментальных точках нет.

Расчетные точки по уравнению (1) с указанными коэффициентами совпали с экспериментальными только в интервале В/Ц=0,5-1,0. (рис. 1, кривая 1).

При В/Ц=0,4 экспериментальная прочность выше активности (марки) цемента в 1,12 раза. В то время как по кривой 1 прочность превысила активность цемента в 1,2 раза, т.е. кривая 1 прогнозирует возможность получения прочности бетона в 1,2 раза выше активности цемента. И хотя в [3] приводятся сведения о том, что при В/Ц=0,4 прочность бетона может превышать активность цемента в 1,2 раза, однако в экспериментальных исследованиях на цементе марки 42,5, гранитном щебне 5-20 мм и строительном песке без каких-либо добавок с уплотнением на стандартной виброплощадке в условиях заводской лаборатории не удалось получить такого превышения. Опытные образцы показывали прочность 47±1 МПа при расходах цемента 475 кг и воды 475*0,4=190 л, а также при расходах цемента 550 кг и воды 550*0,4=220 л.

После того как была исключена из моделирования экспериментальная точка с В/Ц=0,3, были получены другие коэффициенты уравнения (1), а именно: a=5,5; b=0,84;
с=-3,4 с максимумом Rб/Rц при В/Ц=0,39. На рис. 1 с этими коэффициентами показана кривая 2, по которой величина Rб/Rц совпала с экспериментальной при В/Ц=0,4, а также и с другими точками в интервале В/Ц=0,4-1,0.

Формула для нахождения В/Ц по заданным Rб и Rц выводится из решения уравнения (1) относительно В/Ц = х путем преобразования его в квадратное уравнение:

a*y*x2 + (c*y-1)*x +b*y=0,

решение которого приводит к формуле:

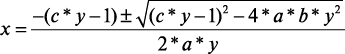. (2)

Для упрощения расчетов кривая 2 на рис. 1 разбита на две части – гиперболу y=a/x+b в интервале В/Ц=0,5-1,0 и прямую y=a*x+b в интервале В/Ц=0,4-0,5.

При моделировании в интервале В/Ц=0,5-1,0 получены коэффициенты гиперболы: a=0,67; b= -0,34. Гипербола с этими коэффициентами показана на рис. 1 под номером 3. Расчет требуемого В/Ц для задаваемых показателей Rб и Rц упрощается и находится по формуле: x=a/(y-b), где: х=В/Ц больше 0,5, у=Rб/Rц меньше 1. Или:

В/Ц= 0,67/(Rб/Rц +0,34). (3)

Для уравнения прямой y=a*x+b в интервале В/Ц=0,4-0,5 получены коэффициенты: a=-1,2; b=1,6 (на рис. 1 линия 4), а требуемое В/Ц при Rб/Rц=1-1,12 находится по формуле: x=(y-b)/a. Или:

В/Ц=(1,6 – Rб/Rц)/1,2. (4)

Что касается интервала В/Ц=0,3-0,4, то в этом интервале нельзя найти расчетным путем прочность бетона для заданного В/Ц, т.к. в нем появляются пределы В/Ц, при которых прочность бетона достигает максимума. При дальнейшем понижении В/Ц прочность начинает снижаться от невозможности укладывать бетонную смесь без пустот. Предельные В/Ц можно отодвигать в сторону меньших значений повышением расходов воды и цемента, правильным подбором зернового состава крупного (щебень или гравий) и мелкого (песок) заполнителей и их соотношения, применением добавок-пластификаторов повышенной эффективности и совершенствованием методов приготовления, укладки и уплотнения бетонной смеси, а также режимов твердения бетона. Все это применяется в современной практике, и именно поэтому мы не видим понижения прочности бетона от снижения В/Ц.

Чтобы найти какую-либо закономерность изменения прочности от снижения В/Ц в интервале 0,4-0,3 для данных конкретных материалов и конкретной технологии необходимо проводить собственное экспериментальное исследование с изготовлением как минимум пяти опытных замесов с В/Ц=0,3; 0,325; 0,35; 0,375; 0,4.

График на рис. 1 дает хорошую ориентировку для нахождения требуемого В/Ц, чтобы получить задаваемую прочность на данном конкретном цементе с той или иной маркой, но не позволяет видеть необходимые расходы цемента.

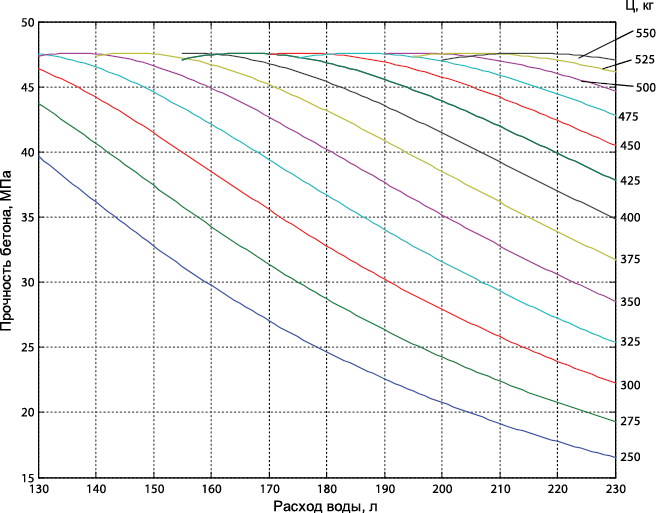
Для того чтобы построить график зависимости прочности бетона от расходов воды и цемента конкретной марки, уравнение (1) было преобразовано в следующее выражение:

Rб=Rц/(a*В/Ц+b*Ц/В+с). (5)

Для построения графика был создан в Матлабе соответствующий m-файл, в котором в качестве переменой величины принят расход воды В=130-230 л/куб.м бетона, при расходах цемента Ц=250-550 кг/куб. м с шагом 25 кг.

Авторскую формулу (5) нельзя ввести в m-файл, т.к. Матлаб читает только латиницу. В m-файле формула (5) имеет вид:

Rb=Rc/(a*W/C+b*C/W+c),

где: Rb=Rб, Rc=Rц, W=В, C=Ц.

Полученный график для заданной марки Rц=42,5 МПа при a=5,5; b=0,84; с=-3,4 (коэффициенты кривой 2 на рис. 1) показан на рис. 2.

По графику (рис. 2) без всяких расчетов видно, что одинаковую прочность, например 35 МПа, можно получить при Ц=375 кг и В=215 л (В/Ц=0,573), а также при Ц=350 кг и В=200 л (В/Ц=0,571), или при Ц=325 кг и В=186 л (В/Ц=0,572).

По формуле (3) для получения Rb=35 МПа при Rc=42,5 МПа:

В/Ц= 0,67/(35/42,5+0,34)=0,575.

Если бы марка цемента была не 42,5, а 52,5, то при указанных расходах цемента и воды прочность была бы 35*52,5/42,5=43,2 МПа.

Для получения прочности, например, 45 МПа (Rб/Rц больше 1) требуемое В/Ц по формуле (4): В/Ц=(1,6 – 45/42.5)/1,2=0,45.

В заключение следует отметить, что представленные формулы прочности и графики не учитывают консистенцию бетонной смеси, которая, по опытным данным, незначительно влияет на прочность бетона. По данным, приведенным в [3], при одном и том же В/Ц прочность образцов из плотно уложенных (с коэффициентом уплотнения не менее 0,98) жестких смесей на 1-5% выше прочности образцов из пластичных смесей.

С развитием технологии бетона факторов, положительно влияющих на прочность бетона и другие свойства, становится все больше и больше, так как расширяется ассортимент цементов, заполнителей и добавок, возникают, как отмечалось выше, новые технологические приемы приготовления, укладки и выдерживания бетонной смеси, позволяющие отодвигать предельные В/Ц в сторону все меньших и меньших значений. Поэтому для конкретных материалов и технологий необходимо уточнять расчетные В/Ц путем изготовления и испытания опытных образцов с В/Ц, отличающимся от расчетного на ±0,025, ±0,05, и по интерполяции находить требуемое, а также экспериментально уточнять расходы материалов для получения необходимой консистенции бетонной смеси.

Библиографический список

1. Шумков А.И., Математическая модель закона водоцементного отношения в производстве тяжелого бетона // Технологии бетонов, №3-4, 2011. shumkov-a@ya.ru.

2. Домокеев А.Г. Строительные материалы, – Москва: Высшая школа, 1989.

3. Баженов Ю.М. Технология бетона, Ассоциация строительных вузов, – Москва, 2002.

4. Райхель В., Конрад Д. Бетон, часть 1, – Москва: Стройиздат, 1979.